- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:23.
- Naposledy zmenené 2025-01-23 12:44.
Hodnota P je štatistické meranie, ktoré vedcom pomáha určiť, či je ich hypotéza správna. Hodnota P sa používa na určenie, či sú výsledky ich experimentu v rozsahu hodnôt, ktoré sú pre študované veci normálne. Obvykle, ak hodnota P súboru údajov klesne pod určitú vopred stanovenú hodnotu (napríklad 0,05), vedci odmietnu nulovú hypotézu svojho experimentu - inými slovami, vylúčia hypotézu, kde experimentálna premenná má žiadny významný vplyv. na výsledok. Dnes sa hodnoty p zvyčajne nachádzajú v referenčných tabuľkách výpočtom chi štvorcovej hodnoty.
Krok

Krok 1. Určte očakávané výsledky svojho experimentu
Keď vedci experimentujú a skúmajú výsledky, zvyčajne už majú predstavu o normálnych alebo bežných výsledkoch vopred. To môže byť založené na výsledkoch predchádzajúcich experimentov, spoľahlivých súboroch pozorovacích údajov, vedeckej literatúre a/alebo iných zdrojoch. V prípade experimentu určte očakávaný výsledok a napíšte ho ako číslo.
Príklad: Predpokladajme, že predchádzajúca štúdia ukázala, že na národnej úrovni boli lístky na prekročenie rýchlosti vydávané častejšie červeným autám než modrým automobilom. Predpokladajme, že priemerný výsledok na národnej úrovni ukazuje pomer 2: 1, pričom pomer červených automobilov je vyšší. Chceme zistiť, či má rovnakú tendenciu aj polícia v našom meste, a to rozborom lístka na prekročenie rýchlosti vydaného políciou v našom meste. Ak by sme vzali náhodnú vzorku 150 lístkov na prekročenie rýchlosti, ktoré dostali červené aj modré autá v našom meste, očakávali by sme to 100 pre červené auto a 50 pre modré autá, ak policajná jednotka v našom meste dá lístok podľa porovnania na národnej úrovni.

Krok 2. Určte svoje experimentálne pozorovania
Teraz, keď ste určili svoju očakávanú hodnotu, môžete spustiť experiment a nájsť skutočnú hodnotu (alebo pozorovanie). Výsledok znova zapíšte ako číslo. Ak manipulujeme s niektorými experimentálnymi podmienkami a pozorované výsledky sa líšia od očakávaných výsledkov, existujú dve možnosti: Buď sa to stalo náhodou, alebo bola príčinou tohto rozdielu naša manipulácia s experimentálnymi premennými. Účelom zistenia hodnoty p je v zásade zistiť, či sa pozorované výsledky líšia od očakávaných výsledkov do bodu, v ktorom nemožno odmietnuť nulovú hypotézu-hypotézu, že neexistuje žiadny vzťah medzi experimentálnou premennou a pozorovanými výsledkami.
Príklad: Predpokladajme, že v našom meste náhodne vyberieme 150 lístkov na prekročenie rýchlosti, ktoré budú udelené červeným aj modrým autám. Dostaneme 90 lístok na červené auto a 60 pre modré auto. To sa líši od výsledku, ktorý sme očakávali, tj 100 a 50. Spôsobila naša experimentálna manipulácia (v tomto prípade zmena zdroja údajov z národného na miestny) nejakú zmenu vo výsledkoch, alebo mala naša mestská polícia rovnaké tendencie ako národná úroveň a my sme len pozorovali zhodu? Hodnota p nám pomôže ju určiť.

Krok 3. Určte stupne voľnosti experimentu
Stupne voľnosti sú mierou miery variability v štúdii, ktorá je určená počtom kategórií, ktoré skúmate. Rovnica pre stupne voľnosti je Stupne voľnosti = n-1, kde n je počet kategórií alebo premenných analyzovaných vo vašom experimente.
-
Príklad: Náš experiment má dve kategórie výsledkov: jednu pre červené auto a jednu pre modré auto. V našom experimente teda máme 2-1 = 1 stupeň voľnosti.
Ak porovnáme červené, modré a zelené autá, budeme mať
Krok 2. stupne voľnosti a pod.

Krok 4. Porovnajte očakávané výsledky s pozorovanými výsledkami pomocou chi na druhú
Chi na druhú (napísané x2) je číselná hodnota, ktorá meria rozdiel medzi očakávanými a pozorovanými hodnotami z experimentu. Rovnica pre chí na druhú je: X2 = ((o-e)2/e), kde o je pozorovaná hodnota a e je očakávaná hodnota. Sčítajte výsledky tejto rovnice pre všetky možné výsledky (pozri nižšie).
- Všimnite si, že táto rovnica používa operátor (sigma). Inými slovami, musíte vypočítať ((| o-e | -.05)2/e) pre každý možný výsledok potom sčítajte výsledky, aby ste získali hodnotu chi na druhú. V našom prípade máme dva výsledky - auto, ktoré dostane červený alebo modrý lístok. Môžeme teda vypočítať ((o-e)2/e) dvakrát - raz pre červené auto a raz pre modré auto.
-
Príklad: Pripojme naše očakávané hodnoty a pozorovania do rovnice x2 = ((o-e)2/e). Pamätajte si, že kvôli operátorovi sigma musíme vypočítať ((o-e)2/e) dvakrát - raz pre červené auto a raz pre modré auto. Kroky spracovania sú nasledujúce:
- X2 = ((90-100)2/100) + (60-50)2/50)
- X2 = ((-10)2/100) + (10)2/50)
- X2 = (100/100) + (100/50) = 1 + 2 = 3.

Krok 5. Vyberte úroveň významnosti
Teraz, keď poznáme stupne voľnosti našej experimentálnej súpravy a štvorcovú hodnotu chi, je tu len posledná vec, ktorú musíme urobiť, kým nájdeme svoju hodnotu p-musíme určiť úroveň významnosti. Úroveň významnosti je v zásade meradlom toho, ako sme si istí svojimi výsledkami - nízka úroveň významnosti zodpovedá nízkej pravdepodobnosti, že výsledok experimentu bol spôsobený náhodou a naopak. Úroveň významnosti je zapísaná ako desatinné miesto (napr. 0,01), čo zodpovedá percentuálnej pravdepodobnosti, že výsledok experimentu bol spôsobený náhodou (v tomto prípade 1%).
- Podľa konvencie vedci zvyčajne stanovili hodnotu významnosti svojich experimentov na 0,05 alebo 5 percent. To znamená, že experimentálne výsledky, ktoré zodpovedajú tejto hladine významnosti, majú nanajvýš 5% šancu na náhodu. Inými slovami, existuje 95% pravdepodobnosť, že výsledky sú spôsobené manipuláciou experimentálnych premenných s vedcom, a nie náhodou. Pri väčšine experimentov sa 95% spoľahlivosť vzťahu medzi týmito dvoma premennými považuje za úspešnú pri preukazovaní vzťahu medzi týmito dvoma premennými.
- Príklad: V prípade nášho príkladu červeného a modrého auta sa riaďme vedeckou dohodou a určme svoju úroveň významnosti 0, 05.
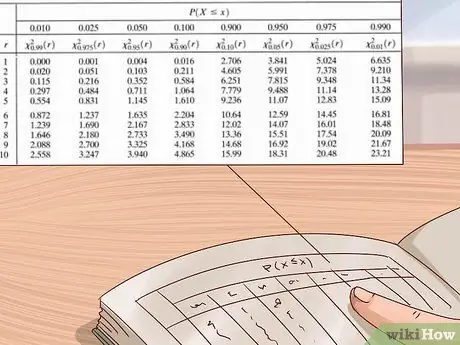
Krok 6. Na odhad hodnoty p použite štvorcovú distribučnú tabuľku čchi
Vedci a štatistici používajú na výpočet hodnôt p pre svoje experimenty veľké tabuľky hodnôt. Táto tabuľka je zvyčajne napísaná tak, že zvislá os vľavo ukazuje stupne voľnosti a horizontálna os v hornej časti ukazuje hodnoty p. Túto tabuľku použite tak, že najskôr nájdete svoje stupne voľnosti a potom budete čítať riadky zľava doprava, kým nenájdete prvú hodnotu, ktorá je väčšia ako hodnota chi na druhú. Pozrite sa na hodnotu p v hornej časti stĺpca-vaša hodnota p je medzi touto hodnotou a ďalšou najväčšou hodnotou (správna hodnota je naľavo od nej).
- Distribučné tabuľky Chi square sú k dispozícii z rôznych zdrojov - dajú sa ľahko nájsť online alebo v učebniciach vedy alebo štatistiky. Ak ho nemáte, použite tabuľku uvedenú na fotografii vyššie alebo bezplatnú online tabuľku, ako je napríklad tá, ktorú poskytuje server medcalc.org tu.
-
Príklad: Naša chi na druhú je 3. Použime teda štvorcovú distribučnú tabuľku chi na fotografii vyššie na nájdenie približnej hodnoty p. Pretože vieme, že náš experiment iba má
Krok 1. stupňa voľnosti, začneme od najvyššej tabuľky. V tomto riadku ideme zľava doprava, kým nenájdeme hodnotu vyššiu ako
Krok 3 - naša hodnota chi na druhú. Prvá hodnota, ktorú nájdeme, je 3,84. Pri pohľade na tento stĺpec vidíme, že zodpovedajúca hodnota p je 0,05. To znamená, že naša hodnota p je medzi 0,05 a 0,1 (ďalšia najväčšia hodnota p v tabuľke).

Krok 7. Rozhodnite sa, či svoju nulovú hypotézu odmietnete alebo obhájite
Keďže ste pre svoj experiment našli približnú hodnotu p, môžete sa rozhodnúť, či nulovú hypotézu experimentu odmietnete (alebo pripomíname, toto je hypotéza, že experimentálna premenná, s ktorou ste manipulovali, nemala žiadny vplyv na výsledky, ktoré ste pozorovali). Ak je vaša hodnota p nižšia ako hodnota významnosti, gratulujeme-dokázali ste, že je vysoká pravdepodobnosť, že existuje vzťah medzi premennými, s ktorými ste manipulovali, a vašimi pozorovaniami. Ak je vaša hodnota p väčšia ako hodnota významnosti, nemôžete s istotou povedať, že výsledky, ktoré pozorujete, sú výsledkom iba náhody alebo manipulácie s vašim experimentom.
- Príklad: Naša hodnota p je medzi 0,05 a 0,1. To znamená, že nie je v žiadnom prípade nižšia ako 0,05, takže bohužiaľ nemôže odmietnuť našu nulovú hypotézu. To znamená, že nedosahujeme minimálnu hranicu 95% spoľahlivosti, ktorú sme stanovili tak, aby sa dalo povedať, že polícia v našom meste dáva lístky na lístky na červené a modré autá v pomere, ktorý sa celkom líši od celoštátneho priemeru.
- Inými slovami, existuje 5-10% šanca, že naše pozorovania nie sú výsledkom zmeny polohy (analýza nášho mesta, a nie celej jeho časti), ale sú to náhody. Keďže hľadáme pravdepodobnosť menšiu ako 5%, nemôžeme povedať, že áno presvedčený že polícia v našom meste má tendenciu dávať lístky na červené autá - existuje malá, ale štatisticky veľmi odlišná možnosť, že túto tendenciu nemajú.
Tipy
- Vedecká kalkulačka výpočty výrazne uľahčí. Kalkulačky môžete vyhľadávať aj online.
- Hodnoty p môžete vypočítať pomocou niekoľkých počítačových programov, vrátane bežne používaného tabuľkového procesora a špecializovanejšieho štatistického softvéru.






