- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Naposledy zmenené 2025-01-23 12:44.
Posun vo fyzike znamená zmenu polohy predmetu. Keď vypočítate výtlak, vypočítate, ako ďaleko je objekt od počiatočného a konečného umiestnenia. Vzorec, ktorý použijete na výpočet výtlaku, závisí od premennej danej problému. Pri výpočte výtlaku postupujte podľa týchto krokov.
Krok
Časť 1 z 5: Výpočet výsledného posunu

Krok 1. Ak je na označenie počiatočných a koncových polôh použitá jednotka vzdialenosti, použite vzorec výsledného posunu
Aj keď sa vzdialenosť líši od výtlaku, výsledný problém s výtlakom hľadá, koľko kilometrov alebo metrov objekt prešiel. Túto jednotku merania použijete na výpočet posunu a vzdialenosti, v akej sa odchýlka polohy objektu od jeho východiskového bodu.
- Výsledný vzorec posunu je zapísaný ako: S = x²+y². S je posunutie. X je prvý smer pohybu objektu a Y je druhý smer pohybu objektu. Ak sa váš objekt pohybuje iba v jednom smere, potom Y = 0.
- Objekt sa môže pohybovať maximálne v dvoch smeroch, pretože pohyb pozdĺž osi sever/juh alebo východ/západ je považovaný za neutrálny pohyb.

Krok 2. Spojte body v poradí pohybu a označte ich od A-Z
Pravítkom nakreslite priamku z bodu do bodu.
- Nezabudnite tiež prepojiť svoj počiatočný bod s koncovým bodom pomocou priamky. Toto je výtlak, ktorý vypočítame.
- Ak sa napríklad predmet pohybuje na východ 300 m a sever 400 m, vytvorí pravouhlý trojuholník. AB bude prvou vetvou trojuholníka a BC bude druhou nohou. AC bude prepona trojuholníka a jeho veľkosť je posunutie objektu. V tomto prípade sú tieto dva smery východ a sever.

Krok 3. Zadajte hodnoty pre x² a y²
Teraz, keď poznáte dva smery pohybu vášho objektu, zadajte hodnoty do príslušných premenných.
Napríklad x = 300 a y = 400. Váš vzorec by mal vyzerať takto: S = 300² + 400²
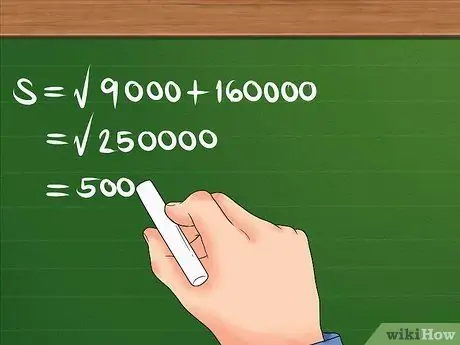
Krok 4. Vypočítajte vzorec pomocou poradia operácií
Najprv odmocninu 300 a 400, potom ich sčítajte a nájdite druhú odmocninu súčtu.
Napríklad: S = 90000 + 160000. S = 250000. S = 500. Teraz viete, že výtlak je 500 m
Časť 2 z 5: Keď je známa rýchlosť a čas

Krok 1. Tento vzorec použite, keď vám problém hovorí o rýchlosti objektu a čase, ktorý trvá
Niektoré matematické úlohy vám nepovedia, ako ďaleko alebo ako sa objekt pohybuje. Posun môžete vypočítať pomocou tejto veľkosti času a rýchlosti.
-
V tomto prípade vzorec vyzerá takto: S = 1/2 (u + v) t.
U = počiatočná rýchlosť objektu alebo rýchlosť, ktorou sa predmet začne pohybovať v určitom smere. V = konečná rýchlosť objektu alebo rýchlosť, ktorou sa objekt pohybuje do svojho konečného umiestnenia. T = čas, ktorý potrebuje objekt na dosiahnutie konečného umiestnenia.
- Príklad: Auto ide po ceste 45 sekúnd (potrebný čas). Auto otáča na západ rýchlosťou 20 m/s (počiatočná rýchlosť) a na konci cesty má rýchlosť 23 m/s (konečná rýchlosť). Vypočítajte výtlak na základe týchto faktorov.

Krok 2. Zadajte požadovanú rýchlosť a čas do príslušných premenných
Teraz, keď viete, ako ďaleko sa auto pohybuje, ako rýchlo sa auto pohybuje na začiatku a na konci, môžete zistiť vzdialenosť od východiskového miesta do konečného miesta.
Váš vzorec by mal vyzerať takto: S = 1/2 (20 + 23) 45

Krok 3. Po vložení hodnôt na správne miesto vypočítajte vzorec
Nezabudnite dodržať poradie operácií, inak budú mať výtlaky za následok veľmi odlišné hodnoty.
- Pre tento vzorec nie je dôležité, či omylom vymeníte počiatočnú a koncovú rýchlosť. Keďže tieto čísla budete najskôr sčítať, nezáleží na tom, kde sú v zátvorkách. Avšak pre iné vzorce bude mať zmena počiatočnej a konečnej rýchlosti za následok rôzne hodnoty posunu.
- Váš vzorec by mal vyzerať takto: S = 1/2 (43) 45. Najprv rozdeľte 43 na 2, čo má za následok 21, 5. Potom vynásobte 21, 5 krát 45, takže výsledok je 967,5 metra. 967, 5 je veľkosť vášho výtlaku alebo to, ako ďaleko sa vaše auto posunulo od východiskového bodu.
Časť 3 z 5: Keď je známa počiatočná rýchlosť, zrýchlenie a čas
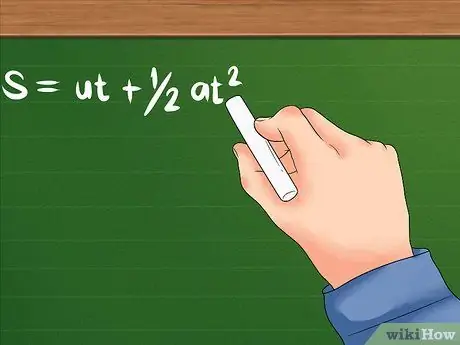
Krok 1. Ak je okrem počiatočnej rýchlosti a času známe aj zrýchlenie, použite upravený vzorec
Niektoré otázky vám povedia iba to, ako rýchlo sa objekt pohybuje na začiatku, ako rýchlo sa objekt začína zrýchľovať a ako ďaleko sa objekt pohybuje. Budete potrebovať nasledujúci vzorec.
- Vzorec pre tento problém je: S = ut + 1/2at². U stále udáva počiatočnú rýchlosť; a je zrýchlenie objektu alebo rýchlosť, ktorou sa jeho rýchlosť začína meniť. T môže znamenať čas potrebný na zrýchlenie objektu alebo určitý čas. Oba budú používať časové jednotky, ako sú sekundy, hodiny a ďalšie.
- Predpokladajme, že auto pohybujúce sa 25 m/s (počiatočná rýchlosť) začne zrýchľovať na 3 m/s2 (zrýchlenie) na 4 sekundy (čas). Aký je zdvihový objem auta po 4 sekundách?

Krok 2. Zadajte hodnoty do vzorca
Na rozdiel od predchádzajúceho vzorca je tu znázornená iba počiatočná rýchlosť, preto nezabudnite zadať správne údaje.
Na základe vyššie uvedených vzorových údajov bude váš vzorec vyzerať takto: S = 25 (4) + 1/2 (3) 4². Pomôže vám to pripočítať zátvorky k veľkosti a času zrýchlenia, ktoré vám pomôžu oddeliť čísla
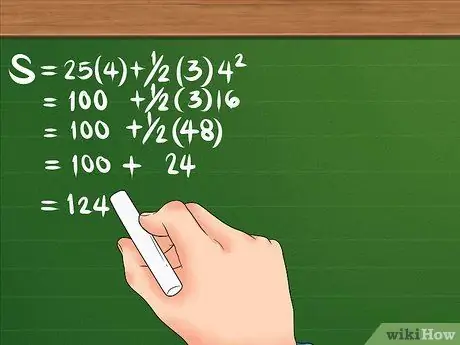
Krok 3. Vypočítajte posunutie tým, že to urobíte v správnom poradí operácií
Rýchly spôsob, ako si pomôcť zapamätať si postupnosť operácií, je somársky most Kur ir Kua ci Kadang Ba wa Juragan Turtles. Toto predstavuje správne poradie: zátvorky, štvorce, násobenie, delenie, sčítanie a odčítanie.
Pozrime sa znova na vzorec: S = 25 (4) + 1/2 (3) 4². Po prvé, štvorec 4, výsledok je 16. Potom vynásobte 16 tromi, čím získate 48; potom tiež vynásobte 25 krát 4, aby ste získali 100. Rozdeľte 48 o 2, aby bola 24. Vaša rovnica by mala vyzerať takto: S = 100 + 24. Keď spojíte dve dohromady, výtlak bude 124 metrov
Časť 4 z 5: Výpočet uhlového posunu

Krok 1. Nájdite uhlový posun, keď sa objekt pohybuje po kruhovej dráhe
Aj keď budete stále počítať posun pomocou priamky, budete musieť nájsť rozdiel medzi počiatočným a koncovým umiestnením objektu pri jeho pohybe v kruhovej dráhe.
- Predstavte si dievča, ktoré sedí na kolotoči. Ako sa točí kolotočom, bude sa pohybovať po kruhovom chodníku. Uhlový posun sa pokúša nájsť najkratšiu vzdialenosť medzi počiatočným a konečným umiestnením, keď sa objekt nepohybuje v priamke.
- Vzorec pre uhlový posun je: = S/r, kde S je lineárny posun, r je polomer a je uhlový posun. Lineárny posun je vzdialenosť, ktorou sa predmet pohybuje po oblúku. Polomer je vzdialenosť objektu od stredu kruhu. Uhlový posun je hodnota, ktorú chceme nájsť.

Krok 2. Pripojte lineárne posunutie a polomer do rovnice
Nezabudnite, že polomer je vzdialenosť od stredu kruhu; niektoré problémy vám povedia priemer kruhu, ktorý musí byť delený 2, aby sa našiel polomer.
- Tu je príklad problému: Dievča jazdí na kolotoči. Sedadlo je 1 meter od stredu kruhu (polomer). Ak sa dievča pohybuje po oblúkovej trajektórii 1,5 metra (lineárny posun), aký je jej uhlový posun?
- Vaša rovnica bude vyzerať takto: = 1,5/1.
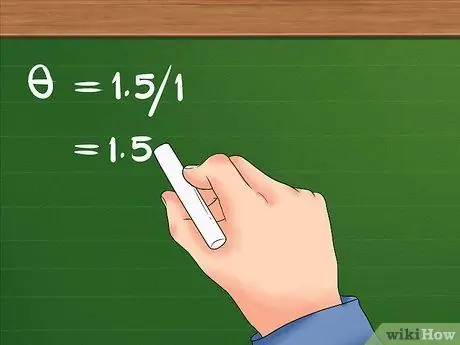
Krok 3. Rozdelte lineárny posun na polomer
Toto rozdelenie bude mať za následok uhlový posun objektu.
- Po delení 1,5 na 1 je výsledok 1,5. Uhlový posun dievčaťa je 1,5 radiány.
- Pretože uhlový posun meria, koľko sa predmet otáča z pôvodnej polohy, mal by byť meraný ako uhol, nie ako vzdialenosť. Radián je jednotka používaná na meranie uhlov.
Časť 5 z 5: Pochopenie migrácie
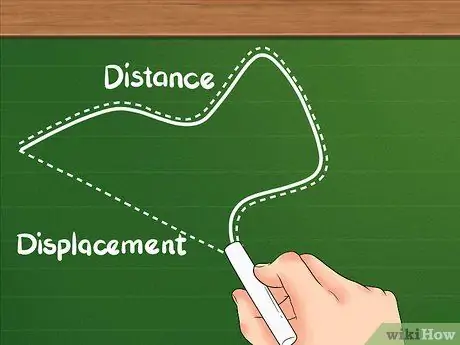
Krok 1. Vedzte, že vzdialenosť má inú definíciu ako posun
Vzdialenosť ukazuje, ako ďaleko je celková vzdialenosť, ktorú objekt prešiel.
- Vzdialenosť je často známa ako skalárne množstvo. Vzdialenosť zobrazuje vzdialenosť, ktorú objekt prešiel, bez ohľadu na smer objektu.
- Ak napríklad prejdete 2 kroky na východ, 2 kroky na juh, 2 kroky na západ a potom 2 kroky na sever, vrátite sa do východiskovej polohy. Napriek tomu, že ste prešli súčtom vzdialenosť Len 10 krokov od vás hýbať sa 0 krokov, pretože vaša konečná poloha je rovnaká ako východisková poloha (vaša cesta pripomína pole).

Krok 2. Pochopte, že výtlak je rozdiel medzi dvoma miestami
Posun nie je celkový súčet pohybu ako vzdialenosť; smeny sa zameriavajú na oblasť medzi vašimi počiatočnými a koncovými polohami.
- Posun sa nazýva vektorová veličina a ukazuje zmenu polohy objektu zvážením smeru pohybu objektu.
- Napríklad kráčate na východ po 5 schodov. Ak sa vrátite na západ po 5 schodoch, budete sa pohybovať v opačnom smere od pôvodného miesta. Aj keď ste prešli 10 schodov, vaša pozícia sa nezmenila; váš výtlak je 0 krokov.

Krok 3. Pamätajte si slová dopredu a dozadu, keď sa pokúšate predstaviť si posun
Pohyb v opačnom smere eliminuje posunutie predmetu.
Predstavte si futbalového trénera tam a späť na vedľajšej koľaji. Keď kričal na hráčov, niekoľkokrát prešiel z ľava do prava. Ak ho sledujete, ako sa pohybuje zľava doprava, sledujete celkovú vzdialenosť, ktorú prešiel. Predpokladajme však, že tréner sa zastaví a porozpráva sa s rozohrávačom na opačnej strane. Ak je pred pohybom v inom bode, ako je pôvodné miesto, potom sledujete pohyb trénera

Krok 4. Vedzte, že výtlak sa meria pomocou priamej dráhy, nie kruhovej
Ak chcete nájsť výtlak, musíte nájsť najkratší a najefektívnejší spôsob výpočtu rozdielu medzi dvoma bodmi.
- Kruhová cesta vás zavedie z počiatočného miesta do konečného, nie je to však najkratšia cesta. Aby ste si to predstavili, predstavte si, že idete po priamke a narazíte na stĺp. Tento stĺp nemôžete preraziť, a tak ho obehnete. Napriek tomu, že je vaša konečná pozícia rovnaká, ako keby ste prerazili stĺp, na dosiahnutie tohto cieľa budete potrebovať ďalšie kroky.
- Napriek tomu, že posun predstavuje priamu cestu, vedzte, že môžete zmerať posunutie objektu, ktorý je aktuálne pohybovať sa v kruhovej dráhe. Tento posun sa nazýva uhlový posun a dá sa vypočítať tak, že sa nájde najkratšia cesta z počiatočného miesta do konečného umiestnenia.

Krok 5. Vedzte, že výtlak môže byť negatívny, na rozdiel od vzdialenosti
Ak sa do konečného umiestnenia dostanete pohybom v opačnom smere, ako je váš pôvodný smer, potom je váš výtlak negatívny.
- Ideme napríklad 5 krokov na východ a potom 3 kroky na západ. Napriek tomu, že sa podľa výpočtu posuniete o 2 kroky z východiskového miesta, váš posun je -2, pretože sa pohybujete v opačnom smere. Vaša vzdialenosť bude vždy kladná, pretože nemôžete počítať dozadu v krokoch, kilometroch atď.
- Negatívny výtlak neznamená, že sa výtlak zmenší. Negatívny znamená, že smer je opačný.

Krok 6. Uvedomte si, že niekedy vzdialenosť a výtlak môžu byť rovnaké
Ak kráčate rovno po 25 schodoch a zastavíte, vzdialenosť, ktorú prejdete, sa bude rovnať výtlaku z vášho pôvodného miesta.
- To platí iba vtedy, ak sa pohybujete z jedného miesta z počiatočného miesta v priamom smere. Žijete napríklad v San Franciscu v Kalifornii a získate novú prácu v Las Vegas v Nevade. Aby ste boli blízko svojej práce, musíte sa presťahovať do Las Vegas. Ak sadnete do lietadla, ktoré letí rovno zo San Francisca do Las Vegas urazíte rovnakú vzdialenosť a výtlak x.
- Ak však pôjdete autom zo San Francisca do Las Vegas, prejdete vzdialenosť x, ale prejdete vzdialenosť y. Pretože jazda autom má zvyčajne rôzny smer (východne od tejto cesty, západne od tejto cesty), budete cestovať na dlhšie vzdialenosti, ako je najkratšia vzdialenosť medzi týmito dvoma mestami.






