- Autor Jason Gerald [email protected].
- Public 2024-02-01 14:15.
- Naposledy zmenené 2025-01-23 12:44.
Proces určovania štvorcových palcov (zapísaný ako v2) vo všetkých oblastiach dvojrozmerných postáv sú zvyčajne dosť jednoduché. V najjednoduchšom prípade, keď je obrázok štvorec alebo štvoruholník, je možné plochu v palcoch na druhú získať pomocou vzorca dĺžka × šírka.
Plochy iných rovinných tvarov (kruhy, trojuholníky atď.) Je možné vypočítať pomocou rôznych matematických vzorcov. V prípade potreby môžete tiež vykonať jednoduchý prevod stôp štvorcových alebo centimetrov štvorcových z palcov na štvorce.
Krok
Metóda 1 z 3: Stanovenie štvorcových palcov na štvorci alebo štvorci
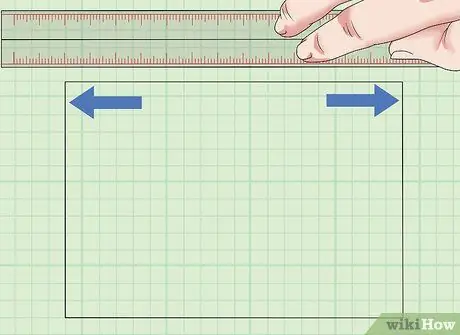
Krok 1. Určte dĺžku oblasti, ktorá sa má merať
Štvorce a obdĺžniky majú 4 rovné strany. Štvorec má štyri strany, ktoré sú rovnako dlhé, zatiaľ čo v obdĺžniku majú rovnakú dĺžku iba protiľahlé strany. Zmerajte jednu stranu štvorca alebo obdĺžnika, aby ste zistili hodnotu dĺžky.
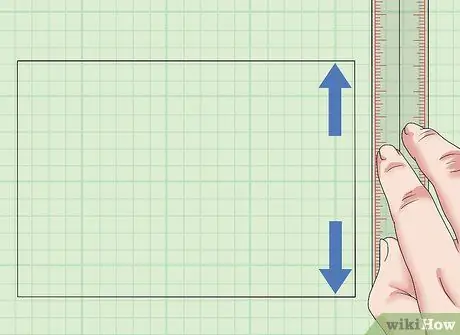
Krok 2. Určte šírku oblasti, ktorá sa má merať
Potom zmerajte jednu zo strán vedľa predtým meranej strany. Táto strana by sa mala stretnúť s prvou stranou v uhle 90 stupňov. Toto je šírka vášho štvorca alebo obdĺžnika.
Pretože všetky štyri strany štvorca majú rovnakú dĺžku, výsledná „dĺžka“sa bude rovnať mierke „šírky“. Na štvorec teda zvyčajne stačí zmerať iba jednu stranu
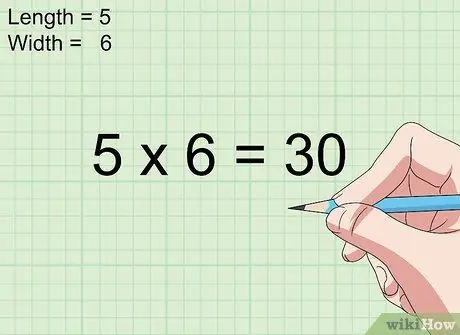
Krok 3. Vynásobte dĺžku a šírku
Jednoducho vynásobte merania dĺžky a šírky, aby ste určili plochu štvorca alebo obdĺžnika v palcoch na druhú.
- Povedzme napríklad, že problém vyžaduje plochu obdĺžnika, ktorý je 4 palce dlhý a 3 palce široký. V tomto prípade je plocha obdĺžnika 4 x 3 = 12 palcov na druhú.
- Všetky strany štvorca majú opäť rovnakú dĺžku strany. Stačí teda zmerať iba jednu stranu a vynásobiť ju samotným číslom (známym tiež ako „kvadratúra“alebo mocnina dvoch), aby ste dostali plochu v palcoch na druhú.
Metóda 2 z 3: Stanovenie štvorcových palcov na iných plochých tvaroch
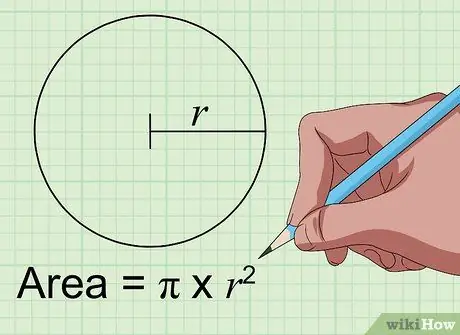
Krok 1. Nájdite oblasť kruhu pomocou vzorca Plocha = pi × r2.
Aby ste našli plochu kruhu v palcoch, stačí poznať vzdialenosť od stredu kruhu k jeho stranám v palcoch. Táto vzdialenosť sa nazýva „polomer“kruhu. Ak ste ho získali, jednoducho zadajte číslo do premennej „r“vo vyššie uvedenom vzorci. Vynásobte samotným číslom a potom vynásobte konštantou pi (3, 1415926 …), aby ste dostali oblasť kruhu v palcoch na druhú.
Kruh s polomerom 4 palce má teda plochu 50,27 palca na druhú, čo je výsledok 3,14 x 16
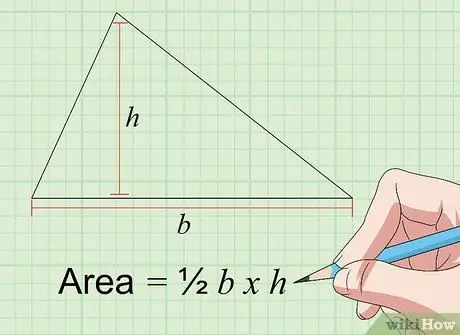
Krok 2. Nájdite oblasť trojuholníka pomocou vzorca Plocha = 1/2 a × t
Plochu trojuholníka v palcoch na štvorce môžete nájsť vynásobením základne ("a") a výšky ("t"), pričom obe sú v palcoch. Základňa trojuholníka je dĺžka jednej z jeho strán, pričom „výška“trojuholníka je vzdialenosť od strany „základne“k rohu trojuholníka oproti nemu v 90-stupňovom uhle. Plochu trojuholníka je možné vypočítať, ak poznáte dĺžky strán základne a výšky troch strán a uhly, ktoré sú proti nim.
Ak teda vyberiete stranu, ktorá je 4 palce dlhá ako základňa, a výška tejto strany základne je 3 palce, plocha trojuholníka je 2 x 3 = 6 palcov na druhú
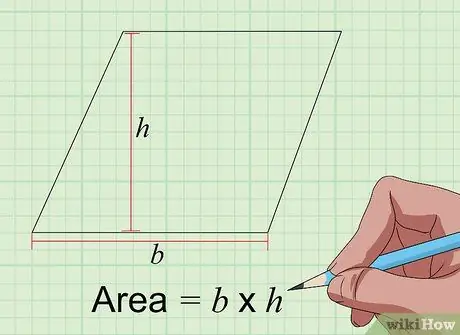
Krok 3. Nájdite oblasť rovnobežníka so vzorcom Plocha = a × t
Rovnobežník je podobný obdĺžniku, ale jeho strany sa nestýkajú v 90-stupňovom uhle. Spôsob, ako nájsť plochu rovnobežníka v palcoch na druhú, je však rovnaký ako v prípade obdĺžnika vynásobením základne výškou v palcoch. Základňa je dĺžka jednej z jej strán, pričom výška je vzdialenosť od boku základne k opačnej strane v uhle 90 stupňov.
Ak je teda dĺžka vybranej strany 5 palcov a po zmeraní výšky je dlhá 4 palce, plocha je 5 x 4 = 20 palcov na druhú
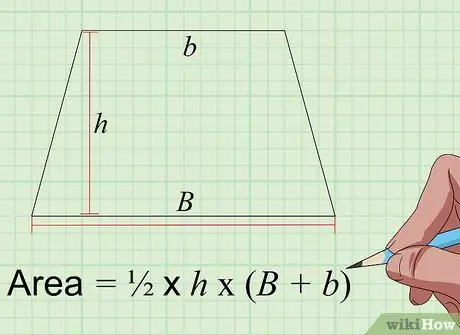
Krok 4. Nájdite oblasť lichobežníka pomocou vzorca Plocha = 1/2 × t × (A+a)
Lichobežník je 4-stranný plochý tvar s jedným párom rovnobežných strán a ostatnými nerovnobežnými stranami. Na výpočet plochy lichobežníka v palcoch na druhú potrebujete poznať 3 merania v palcoch, respektíve dĺžku dlhej rovnobežnej strany („A“), kratšiu rovnobežnú stranu („a“) a výšku lichobežníka („t“), tj. vzdialenosť medzi dvoma rovnobežnými stranami meraná v uhloch 90 stupňov. Pridajte dĺžky dvoch rovnobežných strán, vynásobte ich výškou a potom vydelte dvoma, aby sa plocha lichobežníka v palcoch dostala na druhú.
Ak sú napríklad rovnobežné strany lichobežníka 6 palcov dlhé, krátke rovnobežné strany 4 palce a výška 5 palcov, plocha je x 5 x (6+4) = 25 štvorcových palcov
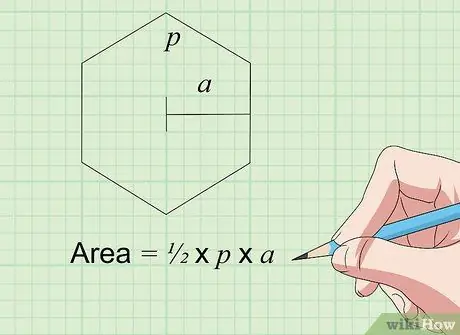
Krok 5. Nájdite oblasť šesťuholníka (šesťuholníka) podľa vzorca Plocha = × K × s
Tento vzorec funguje pre všetky pravidelné šesťuholníky, čo sú ploché tvary, ktoré majú 6 rovnakých strán a 6 rovnakých uhlov. K je obvod alebo dĺžka strany krát 6 (6 x s) pre pravidelný šesťuholník. Premenná a predstavuje apothem, čo je dĺžka od stredu šesťuholníka k jednej z jeho strán (stredový bod strany medzi dvoma uhlami). Výsledok vynásobte a rozdeľte, aby ste našli plochu šesťuholníka.
Ak je teda šesťuholník so všetkými šiestimi stranami dlhý 4 palce (čo znamená K = 6 x 4 = 24) a apotém má dĺžku 3,5 palca, plocha je x 24 x 3,5 = 42 štvorcových palcov
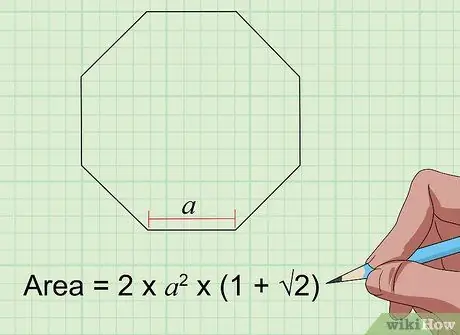
Krok 6. Nájdite oblasť osemuholníka so vzorcom Plocha = 2s² × (1 + 2)
V prípade pravidelného osemuholníka (ktorý má 8 rovnakých strán a 8 uhlov) stačí poznať dĺžku jednej strany (vo vzorci „s“), aby ste našli oblasť. Pripojte hodnoty do vzorca a spracujte ich, aby ste získali plochu osemuholníka.
Ak má váš pravidelný osemuholník dĺžku strany 4 palce, jeho plocha je 2 (16) x (1 + 1, 4) = 32 x 2,4 = 76,8 štvorcových palcov
Metóda 3 z 3: Konverzia iných jednotiek na štvorcové palce

Krok 1. Pred výpočtom zmeňte veľkosť na palce
Ak chcete získať konečnú odpoveď v palcoch na druhú, odporúčame previesť všetky hodnoty, ktoré sa majú vypočítať, na palce (napríklad dĺžku, výšku alebo apotem). Ak sú teda strany štvorca 1 stopa, pred výpočtom plochy ich preveďte na 12 palcov. Na prevod na palce sa bežne používajú nasledujúce prevodné faktory:
- 1 stopa = 12 palcov
- 1 yard = 36 palcov
- 1 centimeter = 0,3937 palca
- 1 meter = 39,3701 palca
- 1 milimeter = 0,0394 palca
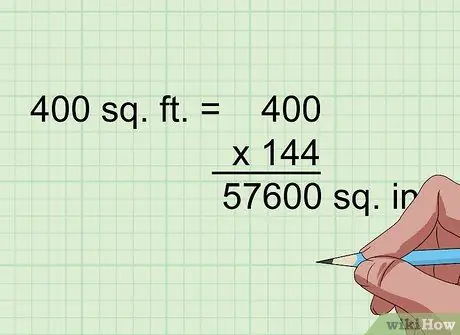
Krok 2. Vynásobením 144 preveďte štvorcové stopy na druhé palce
1 stopa na druhú je 1 stopa na druhú (1 stopa krát 1 stopa); čo znamená, že 12 palcov na druhú sa tiež rovná 12 palcom krát 12 palcov, čo znamená 144 palcov na druhú. Ak má teda plochý tvar plochu v stopách na druhú, jednoducho ho vynásobte 144 a preveďte na štvorce palca.
Napríklad 400 stôp na druhú = 400 x 144 = 57 600 palcov na druhú
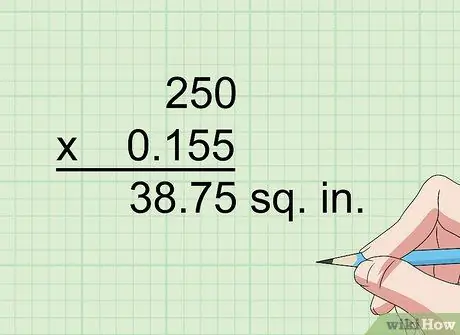
Krok 3. Vynásobením 0,155 preveďte štvorcové centimetre na druhé palce
Jeden centimeter sa rovná 0,394 palca a 0,394 na druhú (0,394 x 0,394) sa rovná 0,155. Ak teda napríklad potrebujete previesť 250 centimetrov na štvorce na palce na štvorce, vynásobením 250 na 0,155 získate 38,75 palca na druhú.






