- Autor Jason Gerald [email protected].
- Public 2024-02-01 14:15.
- Naposledy zmenené 2025-01-23 12:44.
Na výpočet priemernej rýchlosti potrebujete iba celkový výtlak. alebo zmena polohy a celkový čas. Nezabudnite, že rýchlosť tiež počíta smer a rýchlosť objektu, preto do odpovede zahrňte smer, napríklad „sever“, „predok“alebo „doľava“. Ak váš problém s výpočtom rýchlosti zahŕňa aj neustále zrýchľovanie, môžete sa naučiť rýchly spôsob, ako nájsť odpoveď ešte jednoduchšie.
Krok
Metóda 1 z 2: Výpočet priemernej rýchlosti posunu a času

Krok 1. Nezabudnite, že rýchlosť zahŕňa rýchlosť aj smer objektu
Rýchlosť popisuje rýchlosť, ktorou sa mení pozícia objektu. Súvisí to nielen s rýchlosťou pohybu objektu, ale aj s jeho smerom. „100 metrov za sekundu na juh“je iná hodnota rýchlosti ako „100 metrov za sekundu na východ“.
- Veličiny, ktoré majú smer, sa nazývajú vektorové veličiny '. Toto množstvo možno od bezsmernej veličiny nazývanej skalárne množstvo odlíšiť napísaním šípky nad premennou. Zápis v napríklad predstavuje sadzbu, zatiaľ čo zápis v → predstavuje rýchlosť alebo rýchlosť + smer. Notácia použitá v tomto článku predstavuje rýchlosť.
- Vo vedeckých problémoch by ste na vyjadrenie vzdialenosti mali používať metre alebo iné metrické jednotky, zatiaľ čo na každodenné účely môžete používať akékoľvek jednotky, ktoré sa vám páčia.
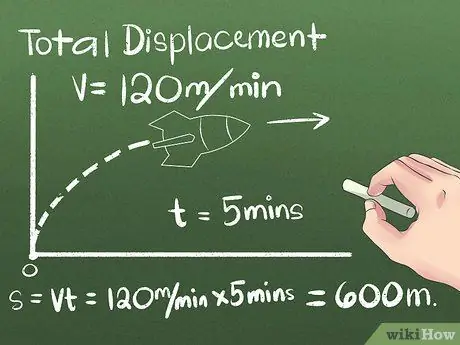
Krok 2. Nájdite hodnotu celkového výtlaku
Posun je zmena polohy objektu alebo vzdialenosti a smeru medzi jeho počiatočným a koncovým bodom. Smer, ktorým sa predmet pohybuje pred dosiahnutím konečnej polohy, je možné zanedbať, pretože sa berie do úvahy iba vzdialenosť medzi počiatočným a koncovým bodom. V prvom prípade použijeme predmet pohybujúci sa konštantnou rýchlosťou v jednom smere:
- Povedzme, že raketa sa pohybuje 5 minút na sever konštantnou rýchlosťou 120 metrov za minútu. Na výpočet konečnej polohy použite vzorec s = vt alebo pomocou praktického myslenia vypočítajte vzdialenosť, ktorú raketa prejde potom (5 minút) (120 metrov/minútu) = 600 metrov severne z východiskového bodu.
- V prípade problémov zahŕňajúcich konštantné zrýchlenie ich môžete vyriešiť pomocou s = vt + at2, alebo použite krátku metódu popísanú v inej časti, aby ste našli odpoveď.
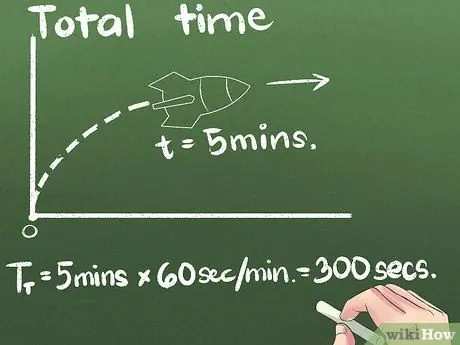
Krok 3. Zistite celkový strávený čas
V našom prípade sa raketa pohybuje dopredu o 5 minút. Priemernú rýchlosť môžete vyjadriť v akejkoľvek jednotke času, ale druhá je medzinárodná vedecká štandardná jednotka. V tomto prípade zmeníme jednotky sekúnd: (5 minút) x (60 sekúnd/minúta) = 300 sekúnd.
Aj vo vedeckých problémoch, ak otázka používa hodinu alebo väčšiu časovú jednotku, bude jednoduchšie najskôr vypočítať rýchlosť a potom konečnú odpoveď previesť na metre/sekundu
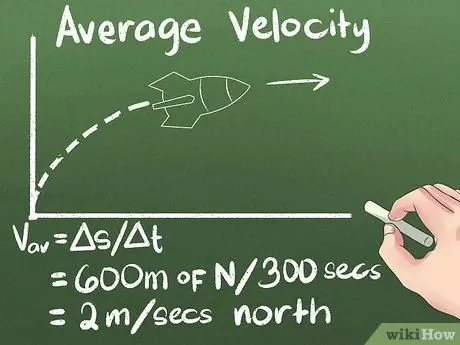
Krok 4. Vypočítajte priemernú rýchlosť ako posun v čase
Ak viete, ako ďaleko sa objekt pohybuje, a ako dlho bude trvať, kým sa k nemu dostanete, budete vedieť, ako rýchlo sa pohybuje. V príklade, ktorý používame, je priemerná rýchlosť rakety (600 metrov severne) / (300 sekúnd) = 2 metre/sekundu na sever.
- Nezabudnite uviesť smer (napríklad „vpredu“alebo „sever“).
- Vo vzorci vav = s/Δt. Symbol delta znamená „zmena“, takže s/Δt znamená „zmena polohy za určité časové obdobie“.
- Priemernú rýchlosť možno zapísať ako vav, alebo ako v s horizontálnou čiarou nad ním.

Krok 5. Vyriešte zložitejšie problémy
Ak predmet zmení smer alebo rýchlosť, nenechajte sa zmiasť. Priemerná rýchlosť je stále „iba“vypočítaná z celkového výtlaku a celkového času. Čo sa stane medzi počiatočným a koncovým bodom, môžete ignorovať. Nasleduje niekoľko príkladov objektu, ktorý cestuje s rovnakým výtlakom a celkovým časom, a teda rovnakou priemernou rýchlosťou:
-
Anna kráča 2 sekundy na západ rýchlosťou 1 meter/s, potom náhle zrýchli na 3 metre/sekundu a pokračuje 2 sekundy v západe. Celkový výtlak je (1 m/s západne) (2 s) + (3 m/s západne) (2 s) = 8 metrov západne. Celkový čas je 2 sekundy + 2 sekundy = 4 sekundy. Priemerná rýchlosť je teda 8 metrov západne/ 4 sekundy = 2 metre/sekundu na západ.
- Bart kráča 3 sekundy na západ rýchlosťou 5 metrov/s, potom sa otočí a 1 sekundu kráča na východ rýchlosťou 7 metrov/s. Pohyb na východ môžeme považovať za „negatívny pohyb na západ“, takže celkový výtlak je = (5 metrov/s na západ) (3 s) + (-7 m/s na západ) (1 s) = 8 metrov. Celkový čas = 4 sekundy. Priemerná rýchlosť = 8 metrov západne / 4 sekundy = 2 metre za sekundu na západ.
-
Charlotte išla na sever 1 meter a potom išla na západ 8 metrov, potom na juh 1 meter. Čas potrebný na dokončenie celej cesty sú 4 sekundy. Nakreslite diagram na kus papiera a uvidíte, že koncový bod je 8 metrov západne od východiskového bodu, takže táto hodnota je posunutie. Celkový čas trvá 4 sekundy, takže priemerná rýchlosť je 8 metrov západne / 4 sekundy = 2 metre/sekundu na západ.
Metóda 2 z 2: Výpočet priemernej rýchlosti pevného zrýchlenia

Krok 1. Zvážte počiatočnú rýchlosť a konštantné zrýchlenie
Povedzme, že náš problém je „Bicykel sa pohybuje doprava rýchlosťou 5 m/s, s konštantným zrýchlením 2 m/s2. Ak sa tento bicykel pohybuje 5 sekúnd, aká je jeho priemerná rýchlosť? “
Ak je jednotka „meter/sekundu2„Aby ste sa mýlili, napíšte to ako„ metre/sekundu/sekundu “alebo„ metre za sekundu za sekundu. “Zrýchlenie 2 metre/sekundu/sekundu znamená, že rýchlosť sa zvyšuje o 2 metre za sekundu každú sekundu.

Krok 2. Na zrýchlenie nájdite konečnú rýchlosť
Zrýchlenie, označené zápisom a, je rýchlosť zmeny rýchlosti (alebo rýchlosti). Rýchlosť sa zvyšuje konštantnou rýchlosťou nárastu. Môžete nakresliť tabuľku pomocou zrýchlenia a nájsť rýchlosť v rôznych časoch počas cesty na bicykli. Túto tabuľku musíme vytvoriť, aby sme našli koncový bod problému (v čase t = 5 sekúnd), ale vytvoríme dlhšiu tabuľku, aby ste tento koncept ľahšie pochopili:
- V počiatočnom bode (čas t = 0 sekúnd) sa bicykel pohybuje rýchlosťou 5 metrov/s.
- Po 1 sekunde (t = 1) sa bicykel pohybuje rýchlosťou 5 metrov/sekundu + pri = 5 metrov/sekundu + (2 metre/sekundu2) (1 sekunda) = 7 metrov za sekundu.
- V čase t = 2 sa bicykel pohybuje doprava rýchlosťou 5+ (2) (2) = 9 metrov/s.
- V čase t = 3 sa bicykel pohybuje doprava rýchlosťou 5+ (2) (3) = 11 metrov/s.
- V čase t = 4 sa bicykel pohybuje doprava rýchlosťou 5+ (2) (4) = 13 metrov/s.
- V čase t = 5 sa bicykel pohybuje vpravo rýchlosťou 5+ (2) (5) = 15 metrov za sekundu.

Krok 3. Na zistenie priemernej rýchlosti použite tento vzorec
Ak a „iba“vtedy, ak je zrýchlenie konštantné, priemerná rýchlosť sa bude rovnať priemernej hodnote súčtu konečných a počiatočných rýchlostí. (vf +vi)/2. Pre náš príklad vyššie uvedeného problému je počiatočná rýchlosť bicykla vi 5 metrov za sekundu. Potom, čo vypočítame, je konečná rýchlosť vf 15 metrov za sekundu. Sčítaním týchto dvoch hodnôt získame (15 metrov/sekundu + 5 metrov/sekundu)/2 = (20 metrov/sekundu)/2 = 10 metrov za sekundu správnym smerom.
- Nezabudnite zahrnúť smer, v tomto prípade „správny“.
- Tento výraz je možné napísať ako v0 (rýchlosť v čase 0 alebo počiatočná rýchlosť) a v (konečná rýchlosť).

Krok 4. Pochopte vzorec priemernej rýchlosti intuitívne
Na nájdenie priemernej rýchlosti môžeme použiť rýchlosť v ľubovoľnom bode a nájsť priemer pre všetky z nich. (Toto je definícia priemeru.) Keďže to vyžaduje kalkul alebo nekonečný čas, porozumiete tomuto vzorcu intuitívnejšie. Namiesto toho, aby ste museli zakaždým brať čas, vypočítajte priemernú rýchlosť dvoch časových bodov a pozrite sa na výsledky. Jeden časový bod je blízko začiatku jazdy, kde ide bicykel pomaly, a ďalší bod je blízko koncového bodu, kde ide rýchlo.

Krok 5. Otestujte intuitívnu teóriu
Pomocou tabuľky vyššie určte rýchlosť v rôznych časových bodoch. Niektoré páry, ktoré spĺňajú naše kritériá, sú (t = 0, t = 5), (t = 1, t = 4) alebo (t = 2, t = 3). Tento vzorec môžete otestovať aj s inými hodnotami t než celými číslami, ak chcete.
Bez ohľadu na to, ktorý pár bodov si vyberiete, priemerná rýchlosť v tom čase bude vždy rovnaká. Napríklad (((5+15)/2), ((7+13)/2) alebo ((9+11)/2) sa všetky rovnajú 10 metrov/s vpravo

Krok 6. Dokončite intuitívne vysvetlenie
Ak použijeme túto metódu so zoznamom každého času, ktorý sme urobili, budeme pokračovať vo výpočte priemeru prvej polovice cesty a druhej polovice cesty. Čas potrebný na pokrytie každej polovice je rovnaký, takže keď skončíme s počítaním, nestratí sa žiadna rýchlosť.
- Pretože obidva páry poskytnú rovnaký výsledok, priemer týchto rýchlostí bude tiež rovnaký. V našom prípade je rýchlosť celku „10 metrov/s doprava“stále 10 metrov/s vpravo.
- Túto hodnotu nájdeme vypočítaním priemeru akéhokoľvek páru, napríklad počiatočnej a konečnej rýchlosti. V našom prípade sú tieto rýchlosti dosiahnuté pri t = 0 a t = 5 a dajú sa vypočítať pomocou vyššie uvedeného vzorca: (5+15)/2 = 10 metrov/s vpravo.

Krok 7. Pochopte tento vzorec matematicky
Ak vám viac vyhovujú dôkazy zapísané ako vzorce, môžete začať so vzorcom na výpočet prejdenej vzdialenosti za predpokladu konštantného zrýchlenia a odtiaľ odvodiť vzorec:
- s = vit + o2. (Technicky s alebo t, alebo zmena polohy a zmena v čase, ale chápali by ste to aj vtedy, keby ste napísali s a t.)
- Priemerná rýchlosť vav definované ako s/t, zadajte preto vzorec v tvare s/t.
- vav = s/t = vi + o
- Zrýchlenie x čas sa rovná zmene celkovej rýchlosti alebo vf - vi. Vo vzorci teda môžeme nahradiť „at“a získať:
- vav = vi + (vf - vi).
- Zjednodušiť: vav = vi + vf - vi = vi + vf = (vf +vi)/2.
Tipy
- Rýchlosť sa líši od rýchlosti, pretože rýchlosť je vektorová veličina, zatiaľ čo rýchlosť je skalárna veličina. Vektorové veličiny zahŕňajú smer aj veľkosť, zatiaľ čo skalárne veličiny zahŕňajú iba veľkosť.
- Ak sa objekt pohybuje v jednej dimenzii, napríklad zľava doprava, môžete použiť kladné číslo na označenie jedného smeru (napríklad vpravo) a záporné číslo na označenie iného smeru (vľavo). Napíšte tento zápis do hornej časti stránky, aby bol ľuďom, ktorí čítajú vašu prácu, jasný.






