- Autor Jason Gerald [email protected].
- Public 2024-01-16 19:56.
- Naposledy zmenené 2025-01-23 12:44.
Rýchlosť je výpočet toho, ako rýchlo sa niečo pohybuje naraz. Ak ste sa niekedy pozreli na rýchlomer pohybujúceho sa auta, uvidíte počítadlo rýchlosti - čím ďalej ihla cestuje, tým vyššia je rýchlosť vozidla. V závislosti od typu informácií, ktoré máte, existuje niekoľko spôsobov, ako vypočítať rýchlosť. Vo všeobecnosti vzorec rýchlosť = vzdialenosť/čas (alebo k = j/w) je najľahší spôsob výpočtu rýchlosti.
Krok
Metóda 1 z 3: Použitie vzorcov na výpočet štandardnej rýchlosti

Krok 1. Nájdite vzdialenosť, ktorú predmet prešiel
Základný vzorec, ktorý väčšina ľudí používa na nájdenie rýchlosti niečoho, sa veľmi ľahko používa. V prvom rade musíte vedieť, „akú vzdialenosť meraný objekt prešiel.“Inými slovami, aká je vzdialenosť medzi počiatočným bodom a koncovým bodom objektu?
Tento vzorec je jednoduchšie pochopiť na príklade. Povedzme, že cestujeme autom na ihrisko „161 kilometrov“. V niekoľkých krokoch môžeme tieto informácie použiť na dokončenie výpočtu vzorca

Krok 2. Nájdite čas, za ktorý objekt prejde túto vzdialenosť
Ďalšia potrebná informácia je, ako dlho trvá objektu, kým sa dostane na určitú vzdialenosť. Inými slovami, ako dlho trvá, kým sa objekt presunie z počiatočného bodu do koncového bodu?
V tomto prípade povedzme, že predmet trvá cca. dve hodiny dostať sa do cieľa.

Krok 3. Vydeľte vzdialenosť časom potrebným na nájdenie rýchlosti objektu
Na poznanie rýchlosti objektu vám stačia tieto dve informácie. Časová vzdialenosť je rovnaká ako rýchlosť objektu.
V tomto prípade 161 kilometrov/2 hodiny = 80,5 kilometra za hodinu.

Krok 4. Nezabudnite na použitú jednotku
Pri odpovedi je veľmi dôležité použiť správne jednotky (napríklad kilometre za hodinu atď.) Bez týchto jednotiek je pre ľudí veľmi ťažké porozumieť významu vašej odpovede. Body môžete stratiť aj vtedy, ak pri zadávaní úloh zo školy použijete nesprávnu jednotku.
Jednotkou rýchlosti je jednotka vzdialenosti k jednotke času. Pretože napríklad merame vzdialenosť v kilometroch a čas v hodinách, použité jednotky sú kilometrov/hod (alebo kilometrov za hodinu).
Metóda 2 z 3: Riešenie ťažších výpočtov

Krok 1. Nájdite niekoľko rôznych premenných na vyriešenie problému vzdialenosti a času
Keď porozumiete základnému vzorcu rýchlosti, môžete ho použiť na iné výpočty ako rýchlosť. Ak napríklad spočiatku poznáte iba rýchlosť objektu a jednu ďalšiu premennú, môžete vyššie uvedený vzorec usporiadať a nájsť neznáme informácie.
-
Povedzme napríklad, že vieme, že vlak ide rýchlosťou 20 kilometrov za hodinu štyri hodiny, ale nevieme, ako ďaleko prešiel. Aby sme to zistili, môžeme vzorec preusporiadať nasledujúcim spôsobom:
-
- rýchlosť = vzdialenosť/čas
- rýchlosť × čas = (vzdialenosť/čas) × čas
- rýchlosť × čas = vzdialenosť
- 20 km/hod × 4 hodiny = vzdialenosť = 80 kilometrov
-

Krok 2. Premeňte používané jednotky podľa potreby
Niekedy môžete rýchlosť vypočítať pomocou určitej jednotky, ale musíte ju previesť na inú jednotku. V takom prípade musíte použiť konverzný faktor, aby ste dostali odpoveď podľa správnych jednotiek. Za týmto účelom jednoducho napíšte vzťah medzi jednotkami v zlomkovej forme a vynásobte ich. Pri násobení podľa potreby obrátte zlomok, aby ste odstránili nežiaduce jednotky. Táto metóda je oveľa jednoduchšia, ako sa zdá!
-
Povedzme napríklad, že v príklade vyššie uvedeného problému potrebujeme odpoveď v kilometroch namiesto v kilometroch. Jedna míľa sa rovná 1,6 kilometru. Konverziu teda môžeme vykonať nasledovne:
-
- 80 kilometrov × 1 míľa/1,6 kilometra = 50 míľ
-
- Pamätajte si, že pretože kilometre sa nachádzajú v spodnej časti zlomku, odoberá kilometre z predchádzajúcej odpovede, takže konečný výsledok používa míle.
- Tento web ponúka funkcie konverzie pre väčšinu bežne používaných jednotiek.

Krok 3. Podľa potreby nahraďte premennú „vzdialenosť“vzorcom vzdialenosti
Objekty sa nepohybujú vždy po rovnej, hladkej dráhe. Ak je to pravda, je možné, že do štandardného vzorca rýchlosti nebudete môcť jednoducho zadať číselnú hodnotu ako jednotku vzdialenosti. Možno však budete musieť nahradiť písmeno j vo vzorci k = j/w vzorcom, ktorý sa podobá vzdialenosti, ktorú objekt prešiel.
-
Povedzme napríklad, že lietadlo sa otáča vzduchom na vzdialenosť 20 míľ 5 krát. Lietadlo dokončilo kolo za pol hodinu. V tomto prípade musíme ešte zistiť celkovú vzdialenosť, ktorú lietadlo prešlo, aby sme mohli určiť jeho rýchlosť. V tomto vzorci môžeme namiesto j použiť vzorec na výpočet vzdialenosti okolo kruhu (vzdialenosť okolo neho). Tento vzorec je obvod = 2πr, kde r = polomer kruhu. Tu je postup, ako to vyriešiť:
-
- k = (2 × × r)/š
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 míľ za hodinu
-

Krok 4. Pochopte, že k = j/w udáva priemernú rýchlosť
Jednoduchý a jednoduchý vzorec, ktorý používame na nájdenie rýchlosti, má jednu nevýhodu. Výsledná hodnota je technicky priemerná rýchlosť. To znamená, že vzorec predpokladá, že objekt, ktorý meriate, používa rovnakú rýchlosť, ako sa pohybuje. Ako uvidíme nižšie, nájdenie rýchlosti objektu v jednom momente bude oveľa ťažšie.
Na ilustráciu tohto rozdielu si predstavte, kedy ste naposledy cestovali autom. Je nepravdepodobné, že budete cestovať rovnakou rýchlosťou, ako cestujete. Cestu však zvyčajne začnete nízkou rýchlosťou a po ceste postupne zvyšujete rýchlosť, zastavujete kvôli červeným svetlám, zápcham atď. Ak na určenie rýchlosti počas jazdy použijete štandardný vzorec rýchlosti, zmeny tejto rýchlosti nemožno zistiť. Dostanete však odpoveď, ktorá ukazuje priemernú rýchlosť všetkých rozdielov rýchlosti, ktorými cestujete
Metóda 3 z 3: Výpočet okamžitej rýchlosti
Poznámka:
Táto časť používa techniky, ktoré sú menej známe ľuďom, ktorí nikdy neštudovali kalkul. Ak potrebujete pomoc, prečítajte si naše články o počte.
Krok 1. Pochopte, že rýchlosť je definovaná ako rýchlosť zrýchlenia
Vysokorýchlostné výpočty rýchlosti sú dosť mätúce, pretože matematici a vedci na opis „rýchlosti“a „zrýchlenia“používajú rôzne definície. Zrýchlenie má dve zložky: „rýchlosť“a „smer“. Rýchlosť sa rovná rýchlosti objektu. Zmena smeru spôsobí zmenu zrýchlenia, ale nie zmenu rýchlosti.
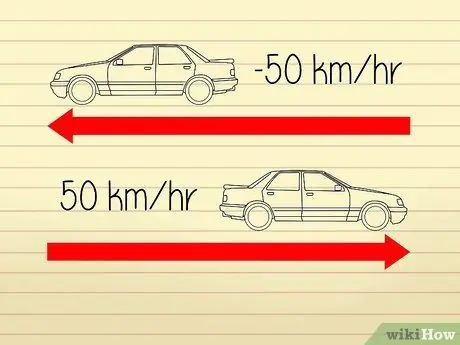
- Povedzme napríklad, že dve autá sa pohybujú opačným smerom. Tachometre na oboch autách ukazujú údaj 50 km/h, takže obaja idú rovnakou rýchlosťou. Keďže sa však autá od seba vzďaľujú, môžeme povedať, že jedno z automobilov má „zrýchlenie“-50 km/h, zatiaľ čo druhé má „zrýchlenie“50 km/h.
- Rovnako ako výpočty okamžitej rýchlosti môžete vykonávať aj výpočty okamžitej akcelerácie.

Krok 2. Na meranie záporného zrýchlenia použite absolútne hodnoty
Objekt môže mať negatívnu rýchlosť zrýchlenia (ak sa pohybuje v negatívnom smere vzhľadom na iný objekt). Negatívna rýchlosť však neexistuje. V tomto prípade teda absolútna hodnota rýchlosti označuje rýchlosť objektu.
Z tohto dôvodu majú vo vyššie uvedenom príklade problém obe autá rýchlosť 50 km/h.
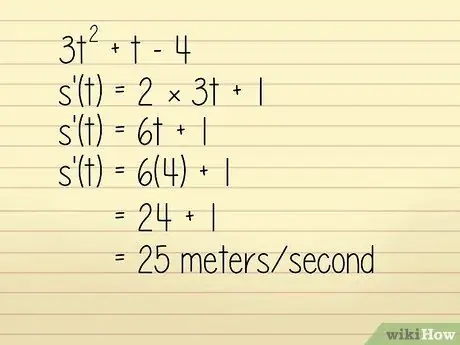
Krok 3. Zoberte deriváciu polohy funkcie
Ak máte funkciu k (w), ktorá ukazuje polohu objektu bez toho, aby ste museli počítať čas, derivácia k (w) ukáže zrýchlenie bez potreby časovania. Stačí do tohto vzorca vložiť hodnotu času, aby sa premenná w (alebo akákoľvek iná hodnota času) zrýchlila podľa tohto času. Odtiaľto môžete ľahko zistiť rýchlosť objektu.
-
Povedzme napríklad, že poloha objektu v jednom metri je popísaná v rovnici 3q2 + w - 4 kde w = čas v sekundách. Chceme poznať rýchlosť objektu pri w = 4 sekundy. V takom prípade to môžete vyriešiť takto:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Teraz zadáme w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 metrov za sekundu. Technicky sa jedná o výpočet zrýchlenia, ale keďže je kladný a smer nie je v otázke uvedený, môžeme ho použiť na nájdenie rýchlosti.
-

Krok 4. Vykonajte integrálnu funkciu zrýchlenia
Zrýchlenie je spôsob merania zmeny zrýchlenia objektu v priebehu času. Táto téma je príliš zložitá na to, aby sa dala v tomto článku úplne vysvetliť. Je však užitočné poznamenať, že keď máte funkciu a (w), ktorá predstavuje zrýchlenie vzhľadom na čas, integrál a (w) vráti výsledok zrýchlenia na základe tohto času. Pamätajte si, že je veľmi užitočné poznať počiatočné zrýchlenie objektu, aby ste mohli definovať konštantu tohto výsledku z nekonečného integrálu.
-
Povedzme napríklad, že objekt má konštantné zrýchlenie (v m/s2 v dôsledku a (w) = -30. Tiež povedzte, že objekt má počiatočné zrýchlenie 10 m/s. Potrebujeme nájsť rýchlosť w = 12 sekúnd. V takom prípade to môžeme vyriešiť takto:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
Aby sme našli C, vyriešime p (w) pre w = 0. Nezabudnite, že počiatočné zrýchlenie objektu je 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, takže p (w) = -30w + 10
-
-
Teraz môžeme zadať w = 12 sekúnd.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Pretože rýchlosť je absolútna hodnota zrýchlenia, rýchlosť objektu je 350 metrov za sekundu.
-
Tipy
- Cvičenie je skvelé! Skúste si vytvoriť vlastnú otázku nahradením čísiel v príklade vyššie uvedeného problému.
- Ak hľadáte rýchly spôsob precvičovania počtu pre lepšiu rýchlosť výpočtu, použite online derivačnú kalkulačku tu a online integrálnu kalkulačku tu.






