Pokiaľ poznáte mieru ďalších dvoch uhlov, je ľahké nájsť tretí uhol trojuholníka. Stačí odpočítať súčet dvoch uhlov o 180 stupňov. Existujú však aj ďalšie spôsoby, ktorými môžete nájsť tretí uhol trojuholníka, ak je tvar problému trochu iný ako obvykle. Ak chcete vedieť, ako nájsť tretí uhol trojuholníka, postupujte podľa nižšie uvedeného návodu.
Krok
Metóda 1 z 3: Použitie mier z ďalších dvoch uhlov
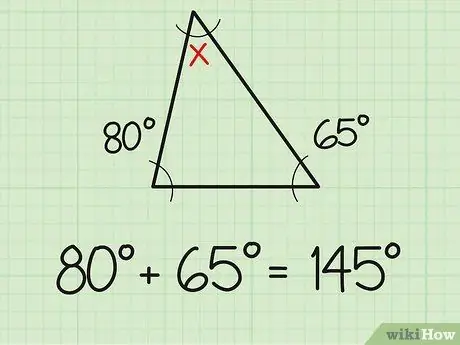
Krok 1. Sčítajte dva známe uhly
Jeden fakt, ktorý by ste mali vedieť, je, že súčet troch uhlov trojuholníka je vždy 180 stupňov. Ak teda už poznáte mieru dvoch uhlov trojuholníka, nájdenie tretieho uhla bude rovnako jednoduché ako jednoduché úlohy sčítania a odčítania. Najprv sčítajte dve miery uhla, ktoré už poznáte. Napríklad dva známe uhly merajú 80 a 65 stupňov. Sčítaním dvoch (80+65) získate 145 stupňov.
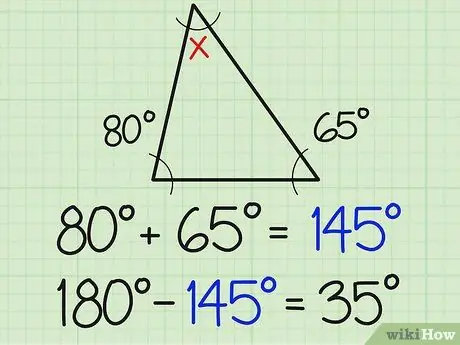
Krok 2. Rozdelte toto číslo na 180
Súčet troch uhlov trojuholníka je vždy 180 stupňov. Preto tretí uhol musí byť 180, keď sa pripočíta k súčtu dvoch známych mier uhla. Vo vyššie uvedenom príklade to znamená 180-154 = 35.
Krok 3. Napíšte svoju odpoveď
Teraz máte odpoveď na tretí uhol (v príklade 35 stupňov). Ak máte stále pochybnosti, presvedčte sa sami. Sčítajte tri uhly a získajte výsledok 180. Ak tak neurobíte, váš výpočet je nesprávny. V tomto prípade 80+65+35 = 180. Ak je to správne, znamená to, že ste problém vyriešili.
Metóda 2 z 3: Použitie premenných
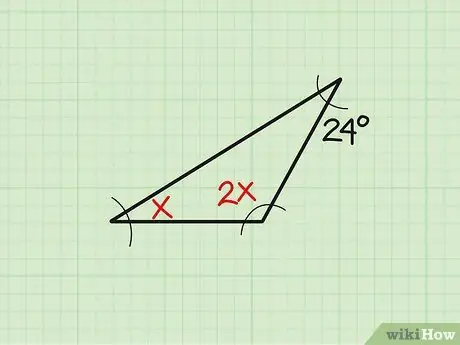
Krok 1. Napíšte problém
Niekedy je veľkosť existujúceho uhla zobrazená v variabilnej forme. Zoberme si tento príklad: „Nájdite uhol„ x “trojuholníka, ak tri uhly merajú„ x “,„ 2x “a 24 v tomto poradí.“Najprv si zapíšte problém.
Krok 2. Sčítajte všetky miery uhla
Princíp, ktorý si musíte zapamätať, zostáva rovnaký. Najprv teda spočítajte tri uhly problému, konkrétne „x+2x+24 = 3x+24“.
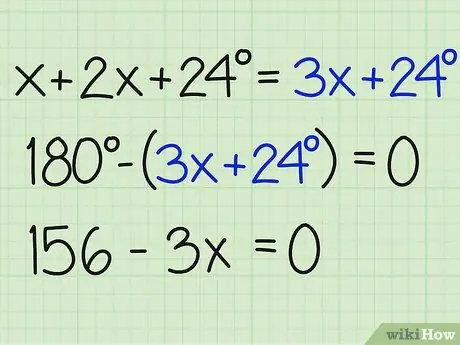
Krok 3. Rozdeľte súčet uhlov o 180
Teraz rozdielom tohto čísla o 180 stupňov vyhľadajte x a nájdite odpoveď na problém. Uistite sa, že rovnicu ukončíte na nulu. Takto je to napísané:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
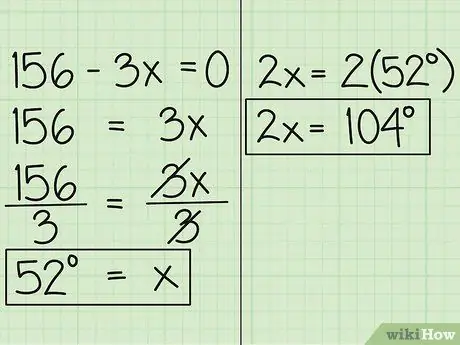
Krok 4. Nájdite hodnotu x
Teraz presuňte premennú na druhú stranu rovnice a dostanete 156 = 3x. Potom delíme rovnicu na 3, takže dostaneme x = 52. To znamená, že miera uhla vyjadrená v x je 52 stupňov. Druhý uhol, vyjadrený v 2x, je 52 stupňov krát 2, čo je 104 stupňov.
Krok 5. Skontrolujte svoje výsledky
Ak sa chcete uistiť, že je vaša odpoveď správna, jednoducho spočítajte tri uhlové miery, na ktoré ste už odpoveď našli. Ak je výsledok 180, znamená to, že vaša odpoveď je správna. V tomto prípade 52+104+24 = 180.
Metóda 3 z 3: Použitie iných metód
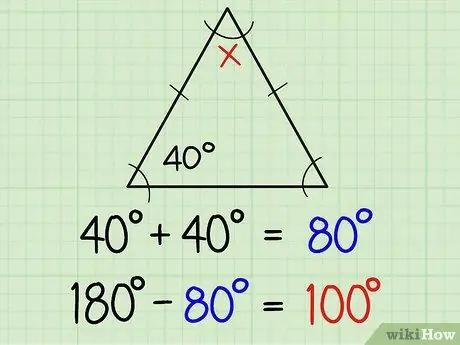
Krok 1. Nájdite uhly rovnoramenného trojuholníka
Rovnomerný trojuholník má dve rovnaké strany a dva rovnaké uhly. Dve rovnaké strany sú zvyčajne označené malou čiarou v strede bočnej čiary, čo znamená, že dva protiľahlé uhly na čiare sú rovnakou mierkou. Ak už poznáte veľkosť jedného uhla, automaticky poznáte aj druhý. Tu je ďalšie vysvetlenie:
Ak má jeden z rovnakých uhlov 40 stupňov, potom druhý má 40 stupňov. Tak môžete nájsť všetky tri uhly s rozdielom medzi súčtom 40+40 (t.j. 80) a 180, alebo inými slovami 180-80 = 100
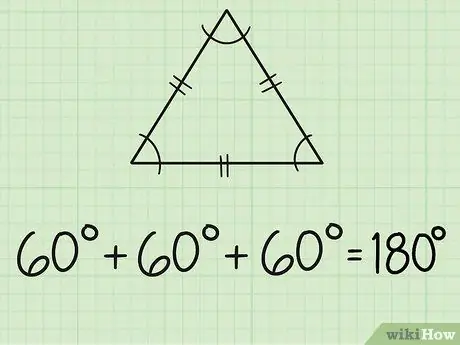
Krok 2. Nájdite uhly rovnostranného trojuholníka
Rovnostranný trojuholník má tri rovnaké strany a tri rovnaké uhly. Každá strana je v strede označená dvoma krátkymi čiarami. Pretože sú všetky tri uhly rovnaké, znamená to, že všetky uhly merajú 60 stupňov, pretože 180/3 = 60.
Krok 3. Nájdite tretí uhol v pravom trojuholníku
Predpokladajme, že dostanete pravý trojuholník s jedným z ostrých uhlov merajúcim 30 stupňov. Pretože je trojuholník pravým uhlom, znamená to, že jeden z uhlov, konkrétne pravý uhol, musí merať 90 stupňov. Potom použite princíp trojuholníka, rozdiel medzi súčtom dvoch uhlov (90+30 = 120) o 180, potom dostanete 180-120 = 60 stupňov.
