- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Naposledy zmenené 2025-01-23 12:44.
Matematiku sa môže naučiť každý, či už je na vyššom stupni školy, alebo si chce len zdokonaliť základy. Po diskusii o tom, ako sa dobre učiť v matematike, vás tento článok naučí základné matematické pokroky a poskytne vám základné prvky, ktoré sa musíte naučiť v každom cvičení. Tento článok bude potom diskutovať o základoch učenia sa aritmetiky, ktoré pomôžu deťom na základnej škole a všetkým, ktorí sa chcú naučiť základy tejto oblasti vedy.
Krok
Časť 1 zo 6: Kľúče k tomu, aby ste sa stali dobrým študentom matematiky

Krok 1. Objavte sa v triede
Keď zmeškáte hodinu, mali by ste sa naučiť koncepty od spolužiakov alebo zo svojej učebnice. Od priateľa nikdy nedostanete textové zhrnutie v takej miere ako od svojho učiteľa.
- Príďte na hodinu včas. Radšej príďte trochu skôr a otvorte zošit na správnom mieste, otvorte učebnicu a vyberte si kalkulačku, aby ste mohli začať, keď je váš učiteľ pripravený učiť.
- Len záškoláctvo, ak ste chorí. Ak vám hodina skutočne chýba, požiadajte svojich spolužiakov, aby zistili, o čom učiteľ hovoril a aké domáce úlohy dostal.

Krok 2. Pracujte so svojim učiteľom
Ak váš učiteľ pracuje na probléme pred triedou, pracujte s učiteľom tak, že problém vyriešite vo svojom zošite.
- Zaistite, aby boli vaše poznámky jasné a ľahko čitateľné. Nepíšte len otázky. Napíšte tiež všetko, čo vám učiteľ povie, čo môže zlepšiť vaše chápanie vysvetľovaných pojmov.
- Vyplňte vzorové otázky, ktoré položil váš učiteľ. Keď učiteľ pracuje po triede, odpovedzte na položené otázky.
- Zúčastnite sa, keď učiteľ vyrieši problém. Nečakajte, kým vám učiteľ zavolá. Ponúknite odpoveď, keď poznáte odpoveď, a zdvihnite ruku, aby ste položili otázku, ak si nie ste istí učeným materiálom.

Krok 3. Urobte si domácu úlohu v ten istý deň, ako máte domácu úlohu
Ak si urobíte domácu úlohu v ten istý deň, koncept je vo vašej mysli stále čerstvý. Niekedy nie je možné dokončiť domácu úlohu v ten istý deň. Pred odchodom do triedy sa uistite, že ste si urobili domácu úlohu.

Krok 4. Ak potrebujete pomoc, pracujte mimo triedu
Navštevujte svojho učiteľa počas prestávok alebo počas úradných hodín.
- Ak máte na škole matematické centrum, zistite jeho otváracie hodiny a požiadajte o pomoc.
- Pripojte sa k študijnej skupine. Dobrá študijná skupina sa spravidla skladá zo 4 alebo 5 ľudí s rôznymi úrovňami schopností. Ak ste študentom matematiky „C“, pripojte sa k skupine 2 alebo 3 študentov s ročníkom „A“alebo „B“, aby ste mohli zlepšiť svoje schopnosti. Vyhnite sa vstupu do skupiny študentov, ktorých známky sú nižšie ako tie vaše.
Časť 2 zo 6: Učenie matematiky v škole

Krok 1. Začnite s aritmetikou
Na väčšine škôl sa študenti učia počítať na základnej škole. Aritmetika pokrýva základy sčítania, odčítania, násobenia a delenia.
- Cvičte otázky. Robiť aritmetické problémy znova a znova je najlepší spôsob, ako si základy správne zapamätať. Vyhľadajte softvér, ktorý vám môže poskytnúť širokú škálu rôznych matematických problémov, s ktorými môžete pracovať. Tiež by ste mali hľadať problémy s časovými rámcami, aby ste zvýšili rýchlosť.
- Aritmetické problémy môžete nájsť aj online a aritmetické aplikácie si môžete stiahnuť do mobilného zariadenia.

Krok 2. Pokračujte s pre-algebrou
Toto cvičenie vám poskytne základné prvky, ktoré budete potrebovať pri neskoršom riešení problémov s algebrou.
- Získajte informácie o zlomkoch a desatinných číslach. Naučíte sa sčítať, odčítať, násobiť a deliť zlomky a desatinné miesta. Pokiaľ ide o zlomky, naučíte sa odčítať zlomky a prekladať kombinované čísla. Pokiaľ ide o desatinné miesta, porozumiete hodnotám miest a v problémoch s príbehom budete môcť používať desatinné miesta.
- Získajte informácie o pomeroch, pomeroch a percentách. Tieto koncepty vám pomôžu naučiť sa porovnávať.
- Predstavte sa v základnej geometrii. Naučíte sa 3D tvary a koncepty. Naučíte sa tiež pojmy ako plocha, obvod, objem a povrch, ako aj informácie o rovnobežných a kolmých čiarach a uhloch.
- Pochopte niekoľko základných štatistík. V pre-algebre váš úvod do štatistiky spravidla obsahuje vizuály, ako sú grafy, bodové grafy, grafy pečiatkových grafov a histogramy.
- Naučte sa základy algebry. To zahŕňa koncepty, ako je riešenie jednoduchých rovníc obsahujúcich premenné, učenie sa o vlastnostiach, ako je distribučná vlastnosť, kreslenie jednoduchých rovníc a riešenie nerovností.
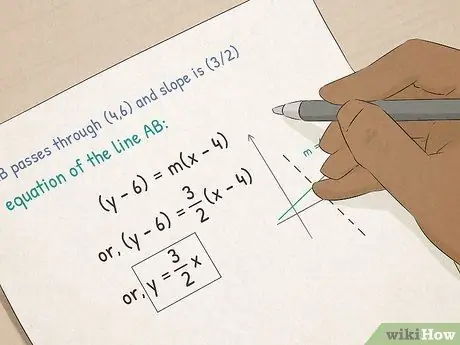
Krok 3. Pokrok v algebre I
V prvom ročníku algebry sa naučíte základné symboly, ktoré algebra obsahuje. Naučíte sa tiež:
- Vyriešte rovnice a nerovnice obsahujúce premenné. Naučíte sa, ako tieto problémy riešiť na papieri a ako ich riešiť pomocou obrázkov.
- Riešiť problémy s príbehom. Budete prekvapení, s akými každodennými problémami sa v budúcnosti stretnete a ktoré vyžadujú schopnosť riešiť problémy s algebraickým príbehom. Pomocou algebry by ste napríklad zistili úrokovú sadzbu, ktorú zarobíte na svojom bankovom účte alebo investícii. Algebru môžete použiť aj na to, aby ste zistili, ako dlho by ste mali cestovať, podľa rýchlosti svojho auta.
- Pracujte s exponentmi. Keď začnete riešiť polynómové rovnice (výrazy, ktoré obsahujú čísla a premenné), pochopíte, ako používať exponenty. To bude pravdepodobne zahŕňať cvičenia s vedeckým zápisom. Keď zvládnete exponenty, môžete sa naučiť sčítať, odčítať, násobiť a deliť polynómové výrazy.
- Vyriešte problémy s druhou a druhou odmocninou. Keď zvládnete túto tému, budete si môcť zapamätať štvorce mnohých čísel. Budete tiež môcť pracovať s rovnicami, ktoré majú odmocniny.
- Pochopte funkcie a grafy. V algebre sa dozviete o grafických rovniciach. Dozviete sa, ako vypočítať sklon čiary, ako vložiť rovnicu do tvaru bodového sklonu a ako vypočítať x-a-y rez priamky pomocou tvaru zachytenia sklonu.
- Zistite sústavu rovníc. Niekedy dostanete 2 rôzne rovnice s premennými xay a pre obe rovnice musíte vyriešiť x alebo y. Našťastie sa naučíte veľa trikov na riešenie týchto rovníc vrátane grafov, substitúcie a sčítania.

Krok 4. Študujte geometriu
V geometrii sa dozviete o vlastnostiach čiar, segmentov, uhlov a tvarov.
- Zapamätáte si množstvo viet a dôsledkov, ktoré vám pomôžu porozumieť pravidlám geometrie.
- Dozviete sa, ako vypočítať plochu kruhu, ako používať Pytagorovu vetu a ako nájsť vzťah medzi uhlami a stranami špeciálneho trojuholníka.
- V budúcich štandardizovaných testoch, ako sú SAT, ACT a GRE, uvidíte veľa otázok týkajúcich sa geometrie.
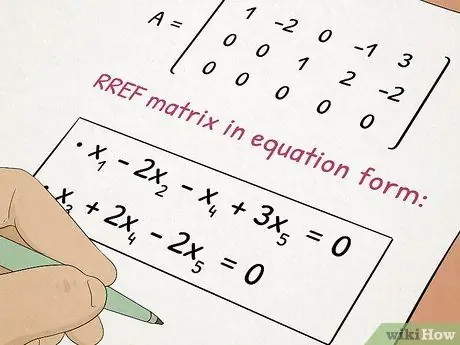
Krok 5. Choďte do triedy Algebra II
Algebra II nadväzuje na koncepty, ktoré ste sa naučili v Algebre I, a pridáva k zložitým témam, ako sú kvadratické rovnice a matice.
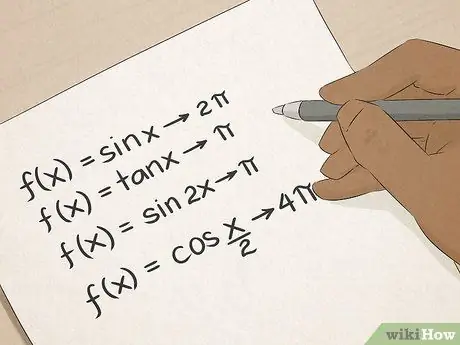
Krok 6. Ovládajte trigonometriu
Poznáte goniometrické výrazy: sínus, kosínus, tangenta a tak ďalej. Trigonometria vás naučí mnoho praktických spôsobov výpočtu uhlov a dĺžok čiar a tieto schopnosti budú neoceniteľné pre ľudí pracujúcich v stavebníctve, architektúre, strojárstve alebo geodézii.
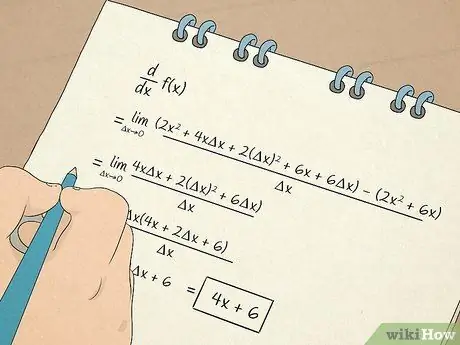
Krok 7. Vykonajte výpočty počtu
Kalkul môže znieť zastrašujúco, ale je to úžasný nástroj na pochopenie buď správania sa čísel, alebo sveta okolo vás.
- Calculus vás naučí funkcie a limity. Uvidíte správanie sa užitočných funkcií vrátane e^x a logaritmických funkcií.
- Naučíte sa tiež počítať a pracovať s derivátmi. Prvá derivácia vám poskytne informácie na základe sklonu dotyčnice k rovnici. Derivát vám napríklad povie, ako rýchlo sa niečo v nelineárnej situácii zmení. Druhá derivácia vám povie, či sa funkcia v určitom intervale zvyšuje alebo znižuje, aby ste mohli určiť konkávnosť funkcie.
- Integrály vás naučia vypočítať plochu pod krivkou a tiež jej objem.
- Kalkul na strednej škole spravidla končí sekvenciami a sekvenciami. Aj keď študenti neuvidia veľa aplikácií pre obvody, obvody sú dôležité pre tých, ktorí študujú diferenciálne rovnice.
Časť 3 zo 6: Základy matematiky-magisterský prírastok

Krok 1. Začnite faktami „+1“
Po pridaní 1 k číslu sa dostanete na najvyššie číslo v číselnom rade. Napríklad 2 + 1 = 3.
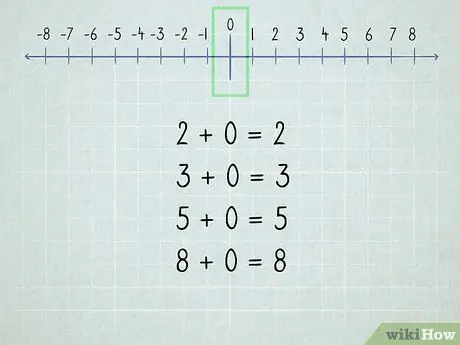
Krok 2. Pochopte nulu
Všetky čísla pridané k nule sú rovnaké číslo, pretože „nula“znamená „žiadne“.

Krok 3. Naučte sa dvojité čísla
Viacnásobné čísla sú problémom, ktorý zahŕňa sčítanie dvoch rovnakých čísel. Napríklad 3 + 3 = 6 je príkladom rovnice obsahujúcej viac čísel.

Krok 4. Pomocou mapovania sa oboznámte s ďalšími riešeniami pridávania
V nižšie uvedenom príklade sa učíte mapovaním toho, čo sa stane, keď pridáte 3 k 5, 2 a 1. Skúste problém „pridať o 2“sami.

Krok 5. Pokračujte, kým číslo nie je viac ako 10
Naučte sa sčítať 3 čísla, aby ste získali číslo väčšie ako 10.
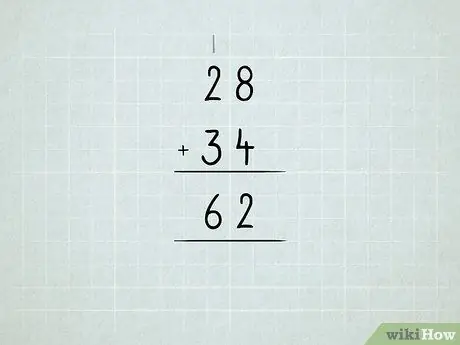
Krok 6. Sčítajte väčšie čísla
Prečítajte si o preskupení jednotiek na desiatky, desiatky na stovky a podobne.
- Najprv sčítajte čísla v pravom stĺpci. 8 + 4 = 12, čo znamená, že máte 1 číslo 10 a 2 číslo 1. Napíšte číslo 2 do stĺpca jednotiek.
-
Do stĺpca desiatok napíšte číslo 1.
-
Sčítajte stĺpec desiatok ako celok.
Časť 4 zo 6: Matematické základy-stratégie znižovania

Krok 1. Začnite s „dozadu 1 číslica
„Odpočítaním 1 od čísla sa vráti 1 číslo. Napríklad 4 - 1 = 3.

Krok 2. Naučte sa odčítať dvojité čísla
Napríklad sčítate čísla 5 + 5, aby ste dostali 10. Stačí napísať rovnicu dozadu a dostanete 10 - 5 = 5.
- Ak 5 + 5 = 10, potom 10 - 5 = 5.
-
Ak 2 + 2 = 4, potom 4 - 2 = 2.

Krok 3. Zapamätajte si rodinu faktov
Ako príklad:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Krok 4. Nájdite chýbajúce čísla
Napríklad _ + 1 = 6 (odpoveď je 5).

Krok 5. Pamätajte si fakt, že odčítanie je na 20

Krok 6. Nacvičte si odčítanie 1-ciferných čísel od 2-ciferných
Odpočítajte čísla v stĺpci tie a znížte čísla v stĺpci desiatok.
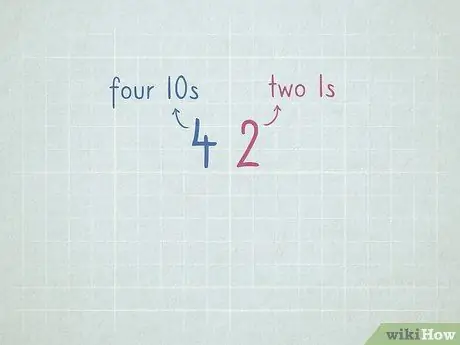
Krok 7. Precvičte si miestnu hodnotu, aby ste sa pripravili na odpočítanie pôžičkou
- 32 = 3 čísla 10 a 2 čísla 1.
- 64 = 6 čísel 10 a 4 čísla 1.
- 96 = _ číslo 10 a _ číslo 1.
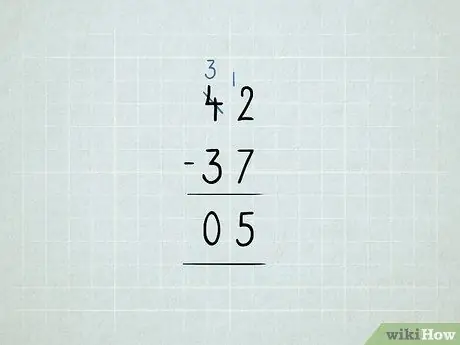
Krok 8. Odpočítajte požičaním
- Chcete odpočítať 42 - 37. Začnite tým, že sa pokúsite odpočítať 2 - 7 v stĺpci jednotiek. Ukázalo sa, že to nefungovalo!
-
Požičajte si číslo 10 zo stĺpca desiatok a umiestnite ho do stĺpca tie. Teraz máte 3 10 namiesto 4 10. Teraz máte 12 1 namiesto 2 1.
-
Najprv odčítajte stĺpec jednotiek: 12 - 7 = 5. Potom skontrolujte stĺpec desiatok. Keďže 3 - 3 = 0, nemusíte si písať číslo 0. Vaša odpoveď je 5.
Časť 5 zo 6: Základy matematiky-majstrovské násobenie

Krok 1. Začnite s číslom 1 a číslom 0
Všetky čísla, ktoré sú vynásobené 1, sú rovnaké ako číslo samotné. Akékoľvek číslo vynásobené 0 sa rovná nule.

Krok 2. Zapamätajte si multiplikačnú tabuľku

Krok 3. Cvičte s problémami s násobením jednej číslice

Krok 4. Vynásobte 2-miestne číslo 1-miestnym číslom
- Vynásobte číslo vpravo dole číslom vpravo hore.
-
Vynásobte číslo vpravo dole číslom vľavo hore.
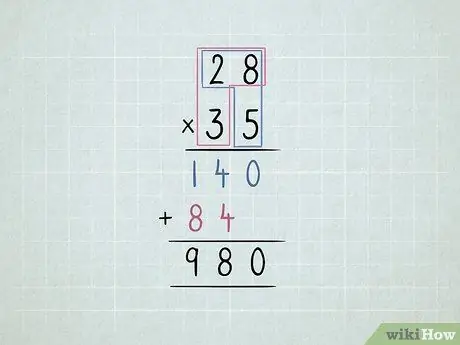
Krok 5. Vynásobte 2 dvojciferné čísla
- Vynásobte číslo vpravo dole číslom vpravo hore a potom číslom vľavo hore.
-
Posuňte druhý riadok o jednu číslicu doľava.
- Vynásobte číslo vľavo dole číslom vpravo hore a potom číslom vľavo hore.
-
Sčítajte všetky stĺpce.
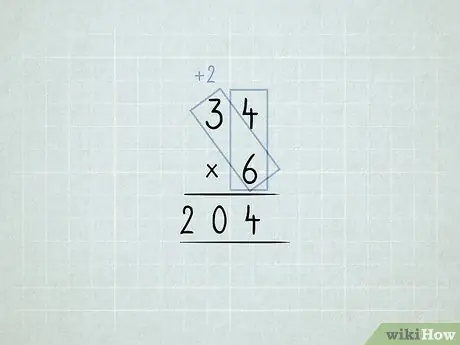
Krok 6. Násobte a preskupte stĺpce
- Chcete vynásobiť 34 x 6. Začnite vynásobením stĺpca jednotiek (4 x 6), ale v stĺpci jednotiek nemôžete mať 24 1 s.
-
Uložte 4 1 s do stĺpca jednotiek. Presuňte 2 10 s do stĺpca desiatok.
-
Vynásobte 6 x 3, čo sa rovná 18. Pridajte 2, ktoré ste presunuli, čo sa rovná 20.
Časť 6 zo 6: Matematické základy-odhalenie problémov s delením

Krok 1. Zamyslite sa nad delením ako proti násobeniu
#* Ak 4 x 4 = 16, potom 16/4 = 4.
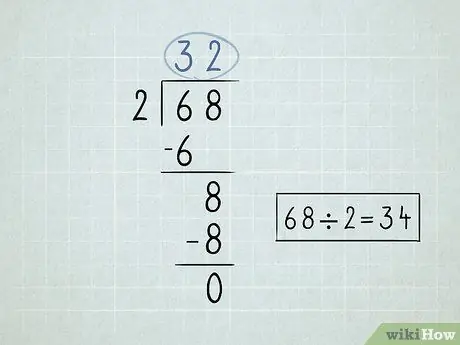
Krok 2. Napíšte svoj problém s delením
- Vydeľte číslo vľavo od symbolu delenia alebo deliteľa prvým číslom pod symbolom deliteľa. Keďže 6 /2 = 3, napísali by ste číslo 3 nad symbol delenia.
-
Vynásobte číslo nad symbolom delenia deliteľom. Výsledok uveďte až na koniec prvého čísla pod symbolom delenia. Pretože 3 x 2 = 6, znížite číslo 6 nadol.
- Odpočítajte 2 zapísané čísla. 6 - 6 = 0. 0 môžete nechať prázdny, pretože spravidla nezačínate číslicami 0.
-
Znížte druhé číslo, ktoré je pod symbolom delenia.
- Rozdeľte číslo, ktoré znížite deliteľom. V tomto prípade 8 /2 = 4. Napíšte číslo 4 nad symbol delenia.
-
Vynásobte číslo vpravo hore deliteľom a znížte ho. 4 x 2 = 8.
-
Odpočítajte tieto čísla. Konečné odčítanie vráti nulu, čo znamená, že ste problém vyriešili. 68 x 2 = 34.

Krok 3. Vypočítajte tiež zvyšok
Niektorí z deliteľov nie sú úplne rozdelení na iné čísla. Ak ste dokončili posledné odčítanie a nemáte žiadne ďalšie čísla na odvodenie, posledné číslo je zvyšok.






