- Autor Jason Gerald [email protected].
- Public 2024-01-16 19:56.
- Naposledy zmenené 2025-01-23 12:44.
Pri štúdiu optických prístrojov je „zväčšenie“predmetu podobného šošovke pomer výšky obrazu, ktorý vidíte, k skutočnej výške predmetu. Napríklad šošovka, vďaka ktorej môže predmet vyzerať veľmi veľký, má „vysoký“faktor zväčšenia, zatiaľ čo šošovka, vďaka ktorej objekt vyzerá ako malý, má „nízky“faktor zväčšenia. Vzorec na zväčšenie objektu sa zvyčajne počíta pomocou vzorca M = (hi/ho) = -(di/do), kde M = zväčšenie, hi = výška obrazu, ho = výška objektu a di a Do = vzdialenosť obrazu a objektu.
Krok
Metóda 1 z 2: Výpočet zväčšenia jedného objektívu
Poznámky: A. konvergujúci objektív v strede širšie ako na okrajoch (ako lupa). a divergentná šošovka na okrajoch širšie ako v strede (ako misa). Výpočet zväčšenia na oboch šošovkách je rovnaký, s jedna dôležitá výnimka. Kliknutím sem prejdete priamo na výnimky pre rozdielne šošovky.
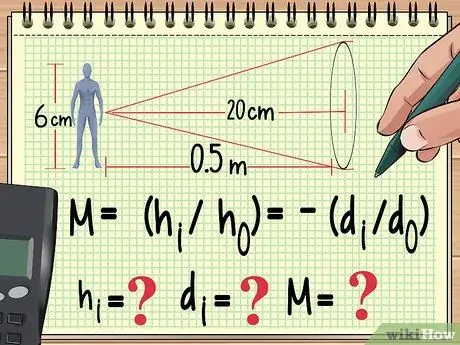
Krok 1. Začnite svojou rovnicou a premennými, ktoré už poznáte
Rovnako ako každý iný problém z fyziky, spôsob, ako vyriešiť problém rozšírenia, je napísať rovnicu, ktorú použijete na jej výpočet. Odtiaľto môžete pracovať späť a nájsť hodnotu premennej, ktorú ste nenašli z rovnice, ktorú používate.
-
Predpokladajme napríklad, že 6 cm vysoká bábika je umiestnená jeden meter od a konvergujúci objektív s ohniskovou vzdialenosťou 20 cm. Ak chceme vypočítať zväčšenie, výšku a vzdialenosť obrazu, môžeme začať písať našu rovnicu nasledovne:
-
- M = (hi/ho) = -(di/do)
-
- Teraz vieme ho (výška bábiky) a do (vzdialenosť bábiky od objektívu). Poznáme aj ohniskovú vzdialenosť objektívu, ktorá sa v tejto rovnici nenachádza. Budeme počítať hidia M.

Krok 2. Použitie rovnice šošovky na získanie di.
Ak poznáte vzdialenosť od objektu, ktorý zväčšujete, a ohniskovú vzdialenosť objektívu, je výpočet vzdialenosti od vytvoreného obrázku pomocou rovnice šošovky veľmi jednoduché. Rovnica šošovky je 1/f = 1/do + 1/di, kde f = ohnisková vzdialenosť šošovky.
-
V tomto príklade môžeme na výpočet d použiť rovnicu šošovkyi. Zadajte hodnoty f a di potom vyriešte rovnicu:
-
- 1/f = 1/do + 1/di
- 1/20 = 1/50 + 1/di
- 5/100 - 2/100 = 1/di
- 3/100 = 1/di
- 100/3 = di = 33,3 cm
-
- Ohnisková vzdialenosť šošovky je vzdialenosť od stredu šošovky k bodu, kde sa v ohnisku prenáša svetlo. Ak ste niekedy zamerali svetlo s lupou na horiace mravce, videli ste to. V otázkach v lekcii bola obvykle uvedená veľkosť tohto hotspotu. V reálnom živote sú tieto špecifikácie zvyčajne napísané na štítku umiestnenom na objektíve.

Krok 3. Výpočet hi.
Potom, čo vypočítate do a Di, môžete vypočítať výšku zväčšeného predmetu a zväčšenie objektívu. Všimnite si dva rovnaké znamienka v rovnici zväčšenia šošovky (M = (hi/ho) = -(di/do)) - to znamená, že všetky časti tejto rovnice sú si navzájom rovnaké, takže môžeme vypočítať M a hi v akomkoľvek poradí chceme.
-
Pre tento príklad problému môžeme vypočítať hi Páči sa ti to:
-
- (hi/ho) = -(di/do)
- (hi/6) = -(33, 3/50)
- hi = -(33, 3/50) x 6
- hi = - 3,996 cm
-
- Upozorňujeme, že výška objektu je tu záporná, čo naznačuje, že obrázok, ktorý uvidíme neskôr, bude obrátený (zhora nadol).

Krok 4. Výpočet M
Poslednú premennú môžete vypočítať podľa rovnice -(di/do) alebo (hi/ho).
-
V nasledujúcom príklade je výpočet M nasledovný:
-
- M = (hi/ho)
- M = (-3, 996/6) = - 0, 666
-
-
Výsledok bude rovnaký aj pri výpočte pomocou hodnoty d:
-
- M = -(di/do)
- M = -(33, 3/50) = - 0, 666
-
- Upozorňujeme, že priblíženie nemá označenie jednotky.
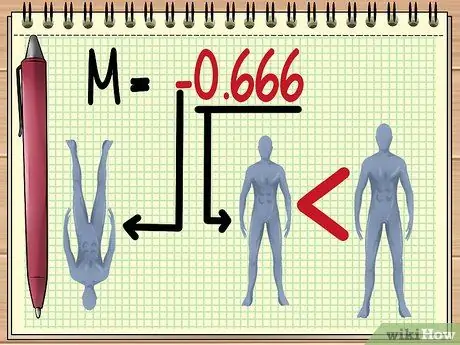
Krok 5. Pochopenie hodnoty M
Akonáhle získate veľkosť hodnoty M, môžete odhadnúť niekoľko vecí o obrázku, ktorý uvidíte cez objektív, a to:
-
Veľkosť.
Čím väčšia je „absolútna hodnota“M, tým väčší bude objekt zobrazený objektívom. Hodnota M medzi 0 až 1 naznačuje, že objekt bude vyzerať menší.
-
Orientácia objektu.
Záporná hodnota znamená, že vytvorený obrázok bude obrátený.
- V tu uvedenom príklade hodnota M -0,666 znamená, že podľa hodnoty existujúcej premennej bude viditeľný tieň bábiky. hore nohami a o dve tretiny menšia ako skutočná veľkosť.
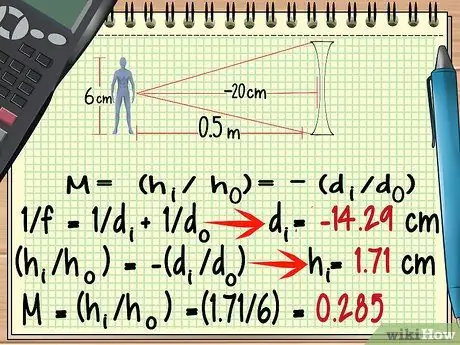
Krok 6. V prípade rozbiehajúcich sa šošoviek použite negatívny ohniskový bod
Napriek tomu, že tvar rozbiehajúcej sa šošovky je veľmi odlišný od tvaru zbiehavej šošovky, jej zväčšenie môžete vypočítať podľa rovnakého vzorca, ako je uvedené vyššie. Výnimky, na ktoré treba pamätať, sú Ohniskový bod rozbiehajúcej sa šošovky je negatívny.
Vo vyššie uvedenom príklade bude mať vplyv na odpoveď, ktorú získate pri výpočte di, takže tomu určite venujte pozornosť.
-
Prepracujme príkladový problém vyššie, až teraz používame rozbiehajúci sa objektív s ohniskovou vzdialenosťou - 20 cm.
Ostatné premenné zostávajú na rovnakej hodnote.
-
Najprv vypočítame di pomocou rovnice šošovky:
-
- 1/f = 1/do + 1/di
- 1/-20 = 1/50 + 1/di
- -5/100 - 2/100 = 1/di
- -7/100 = 1/di
- -100/7 = di = - 14, 29 cm
-
-
Teraz vypočítame hi a M s hodnotou di ten nový.
-
- (hi/ho) = -(di/do)
- (hi/6) = -(-14, 29/50)
- hi = -(-14, 29/50) x 6
- hi = 1,71 cm
- M = (hi/ho)
- M = (1, 71/6) = 0, 285
-
Metóda 2 z 2: Výpočet zväčšenia viacerých šošoviek
Jednoduchá metóda s dvoma šošovkami
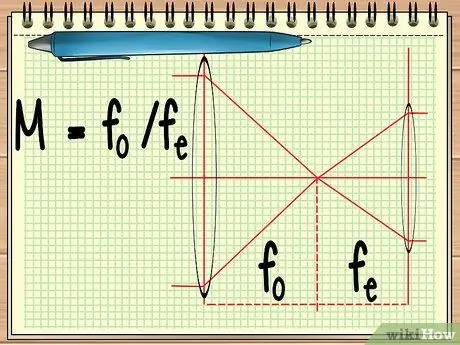
Krok 1. Vypočítajte ohniskový bod dvoch šošoviek
Keď používate nástroj, ktorý sa skladá z dvoch šošoviek usporiadaných vedľa seba (napríklad ďalekohľad alebo ďalekohľad), stačí, ak zistíte ohniskový bod týchto dvoch šošoviek, aby ste vypočítali celkové zväčšenie týchto dvoch šošoviek. to sa dá vypočítať jednoduchou rovnicou M = fo/fe.
V rovnici fo je ohniskovým bodom šošovky objektívu a fe je ústredným bodom okulára. Objektív je veľká šošovka, ktorá je blízko objektu, zatiaľ čo očná šošovka je šošovka, ktorá sa nachádza blízko oka pozorovateľa.

Krok 2. Pripojte informácie, ktoré už máte, do rovnice M = fo/fe.
Akonáhle máte ohniskové body oboch šošoviek, je veľmi ľahké ich vypočítať, - vypočítajte pomer vydelením ohniskovej vzdialenosti šošovky objektívom ohniskovou vzdialenosťou okuláru. Odpoveď, ktorú dostanete, je celkové zväčšenie nástroja.
-
Predpokladajme napríklad jednoduchý ďalekohľad, že je napísané, že ohniskový bod objektívu je 10 cm a ohniskový bod okulára je 5 cm, potom je zväčšenie 10/5 = 2.
Komplikovaná metóda
Krok 1. Vypočítajte vzdialenosť medzi šošovkami a predmetom
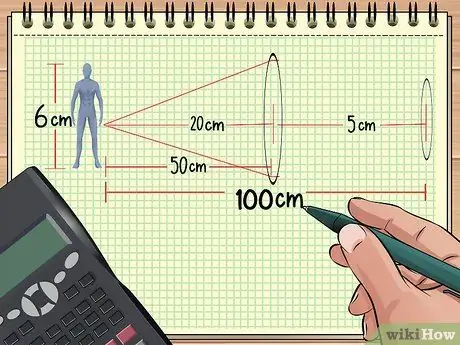
Ak máte pred objektom usporiadané dva objektívy v rade, celkové zväčšenie sa dá vypočítať, ak poznáte vzdialenosť od šošoviek k objektu, veľkosť objektu a ohniskový bod týchto dvoch šošoviek. Rovnako je možné vypočítať aj zvyšok.
Predpokladajme napríklad, že usporiadame predmety a šošovky ako v príklade 1 vyššie: bábika je 50 cm od zbiehajúceho sa objektívu s ohniskovou vzdialenosťou 20 cm. Teraz umiestnite druhý objektív s ohniskom 5 cm vo vzdialenosti 50 cm od prvého objektívu (100 cm od bábiky.) Potom vypočítame celkové zväčšenie pomocou informácií, ktoré sme získali
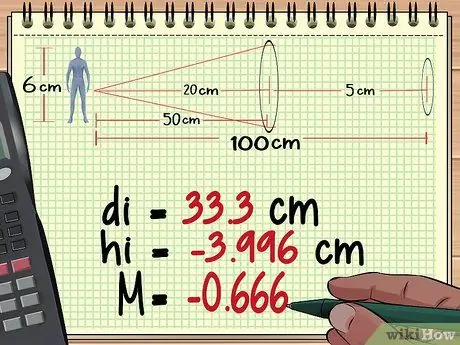
Krok 2. Vypočítajte vzdialenosť, výšku a zväčšenie objektu od objektívu 1
Prvá časť výpočtu zväčšenia viacerých šošoviek je rovnaká ako výpočet zväčšenia jednej šošovky. Začnite objektívom najbližšie k objektu, pomocou rovnice šošovky zistíte vzdialenosť od vytvoreného obrazu a potom pomocou rovnice zväčšenia zistíte výšku a zväčšenie obrázku. Kliknutím sem zobrazíte ďalšie výpočty zväčšenia jedného objektívu.
-
Z našich výpočtov v metóde 1 vyššie sme zistili, že prvý objektív vytvára obraz tak vysoký ako - 3,996 cm, vzdialenosť 33,3 cm za objektívom a pri zväčšení - 0, 666.
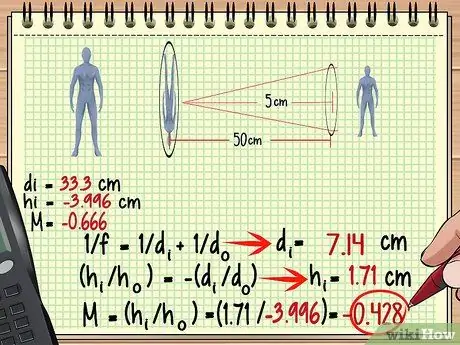
Krok 3. Použite obrázok z prvého objektívu ako objekt z druhého objektívu
Teraz je nájdenie zväčšenia, výšky a ďalších parametrov pre druhý objektív veľmi jednoduché - použite rovnakú metódu, akú ste použili pre prvý objektív, ale tentokrát považujte obrázok za predmet. Nezabudnite, že vzdialenosť obrazu k druhému objektívu nie je vždy rovnaká ako vzdialenosť objektu k prvému objektívu.
-
Vo vyššie uvedenom príklade, pretože obraz je vytvorený 33,3 cm za prvým objektívom, je vzdialenosť 50-33,3 = 16,7 cm pred druhým objektívom. Použime toto meranie a ohniskovú vzdialenosť druhého objektívu na nájdenie obrazu vytvoreného druhým objektívom.
-
- 1/f = 1/do + 1/di
- 1/5 = 1/16, 7 + 1/di
- 0, 2 - 0, 0599 = 1/di
- 0, 14 = 1/di
- di = 7, 14 cm
-
-
Teraz môžeme vypočítať hi a M pre druhý objektív:
-
- (hi/ho) = -(di/do)
- (hi/-3, 996) = -(7, 14/16, 7)
- hi = -(0, 427) x -3, 996
- hi = 1,71 cm
- M = (hi/ho)
- M = (1, 71/-3, 996) = - 0, 428
-
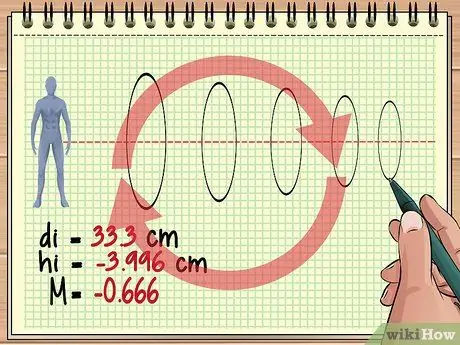
Krok 4. Pokračujte vo výpočte pre ďalšie šošovky
Tento základný prístup je rovnaký, ak sú pred objektom zoradené tri, štyri alebo stovky šošoviek. Pri každom objektíve zvážte ako predmet predmet predchádzajúceho objektívu a pomocou rovnice šošovky a rovnice zväčšenia nájdite požadovanú odpoveď.
Majte na pamäti, že každý nasledujúci objektív môže nepretržite invertovať vytvorený obraz. Napríklad hodnota zväčšenia, ktorú sme získali skôr (-0, 428), naznačuje, že obraz, ktorý uvidíme, je približne 4/10 skutočnej veľkosti objektu, ale je kolmý, pretože obraz z predchádzajúceho objektívu je obrátený
Tipy
- Ďalekohľady spravidla poskytujú vysvetlenie k špecifikáciám zväčšenia vo forme násobku iného čísla. Napríklad ďalekohľad môže byť špecifikovaný ako 8x25 alebo 8x40. Keď je to takto napísané, prvé číslo je zväčšenie ďalekohľadu. Nezáleží na tom, aj keď v uvedenom prípade sú tieto dve čísla rôzne veľké, oba ďalekohľady majú 8 -násobné zväčšenie. Druhé číslo udáva, aký jasný bude obraz vytvorený ďalekohľadom.
- Nezabudnite, že v prípade lupy s jedným objektívom bude zväčšenie záporné, ak je vzdialenosť objektu väčšia ako ohnisková vzdialenosť šošovky. To neznamená, že vytvorený obraz bude menší. V tomto prípade k zväčšeniu stále dochádza, ale vytvorený obraz bude pozorovateľom videný hore nohami (zhora nadol).






