- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:37.
- Naposledy zmenené 2025-01-23 12:44.
Existuje mnoho rôznych tvarov plochých tvarov a existuje mnoho dôvodov, prečo by ste chceli vypočítať plochu: od domácich úloh po odhad, koľko farby je potrebné na premaľovanie obývačky. Nebojte sa, wikiHow má odpoveď! Začnite od kroku 1 nižšie, aby ste vedeli, ako vypočítať plochu rovinného obrázku.
Krok
Metóda 1 zo 7: Štvorec, obdĺžnik a rovnobežník
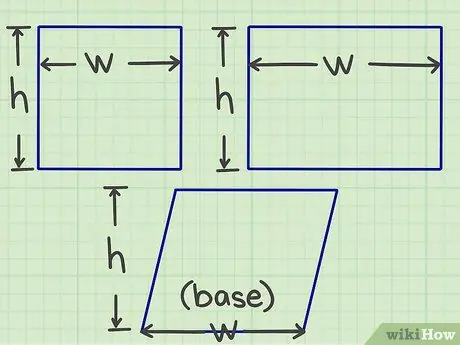
Krok 1. Zmerajte dĺžku a šírku
Začnite merať alebo vypočítať dĺžku a šírku plochého tvaru (alebo inými slovami veľkosť každej z dvoch strán, ktoré sa stretávajú v jednom bode).
- Pre rovnobežník musíte nájsť základňu a výšku, ale zjednodušene povedané, myšlienka je rovnaká ako dĺžka a šírka.
- V skutočnom svete to možno budete musieť zmerať sami, ale pokiaľ ide o domáce úlohy, učiteľ už zvyčajne zapísal čísla spolu s obrázkom tvaru.
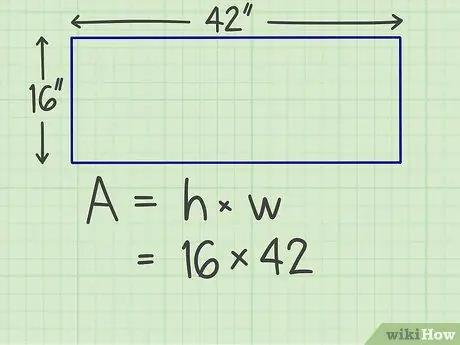
Krok 2. Vynásobte strany
Vynásobte jednu stranu druhou. Predpokladajme napríklad, že máte obdĺžnik so šírkou 16 palcov a dĺžkou 42 palcov, takže musíte vypočítať 16 x 42.
Ak počítate plochu štvorca (predtým štvorca), ušetrite čas tým, že zarovnáte jednu z jeho strán pomocou kalkulačky. Ak strana meria 4 m, výsledok zobrazíte stlačením klávesu 4 a potom štvorcového klávesu na kalkulačke. Štvorec znamená násobenie čísla samotným
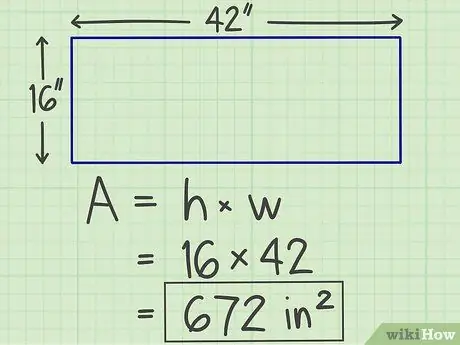
Krok 3. Zapíšte si výsledky
Násobenie, ktoré ste urobili predtým, vytvorí číslo, ktoré je plochou roviny, ktorú vypočítavate, s jednotkou „štvorec“. Obdĺžnik, ktorý sme predtým vypočítali, má teda plochu 672 štvorcových palcov.
Niekedy je táto štvorcová jednotka zapísaná aj ako malá 2, ktorá za názvom jednotky mierne stúpa (podobne ako schopnosti písania)
Metóda 2 zo 7: Trapéz
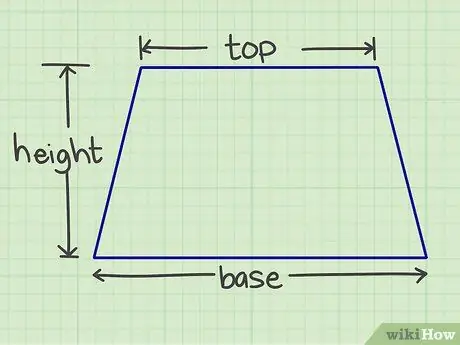
Krok 1. Zmerajte požadované číslo
Budete musieť zmerať základňu, strechu a výšku. Základňa a strecha sú rovnobežné strany, pričom výška je kolmá čiara spájajúca obe rovnobežné strany.
V skutočnom svete to možno budete musieť zmerať sami, ale pokiaľ ide o domáce úlohy, učiteľ už zvyčajne zapísal čísla spolu s obrázkom tvaru
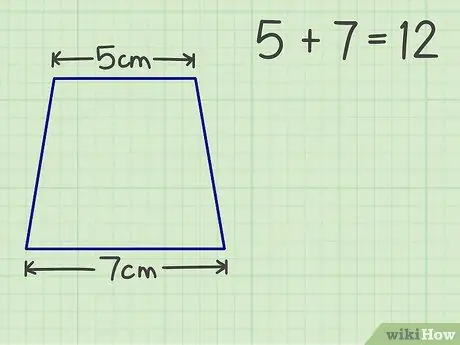
Krok 2. Sčítajte dve rovnobežné strany
Náš lichobežník má napríklad strechu 5 cm a základňu 7 cm. Súčet dvoch rovnobežných strán je 12.
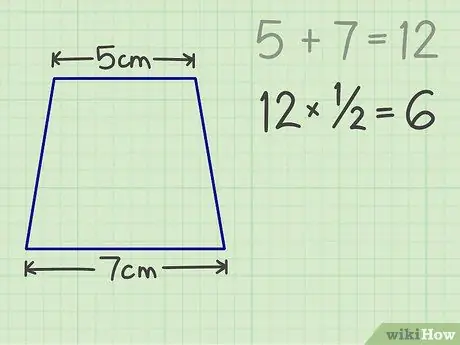
Krok 3. Vynásobte číslo 1/2, výsledkom je 6
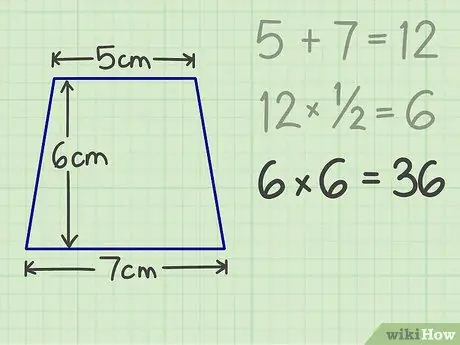
Krok 4. Potom vynásobte výsledok výškou
Ak má napríklad lichobežník výšku 6 cm, konečný výsledok je 36.
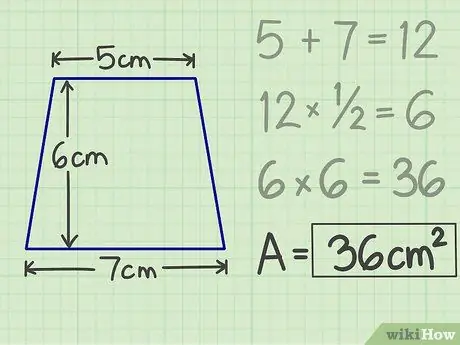
Krok 5. Zapíšte si výsledky
Násobenie, ktoré ste urobili predtým, prinesie číslo, konkrétne oblasť lichobežníka. Takže pre lichobežník so strechou 5 cm, základňou 7 cm a výškou 6 cm je plocha 36 cm štvorcových.
Metóda 3 zo 7: Kruh
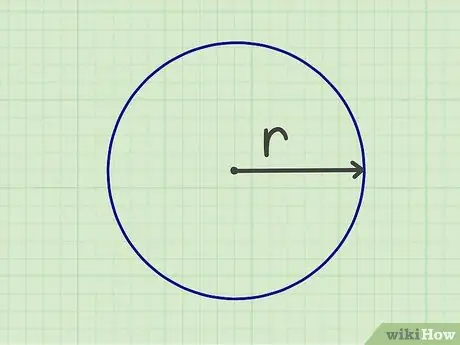
Krok 1. Zmerajte polomer
Aby ste mohli vypočítať plochu kruhu, musíte zmerať polomer. polomer je vzdialenosť od stredu kruhu k jeho okraju. Polomer môžete merať aj zmeraním priemeru (šírky kruhu od okraja k okraju) a potom vydelením čísla dvoma.
V skutočnom svete to možno budete musieť zmerať sami, ale pokiaľ ide o domáce úlohy, učiteľ už zvyčajne zapísal čísla spolu s obrázkom tvaru
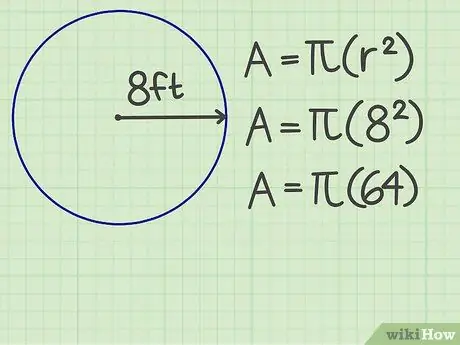
Krok 2. Štvorce prstov
Vynásobte počet polomerov sám. Napríklad polomer kruhu je 8 stôp, takže výsledok je 64.
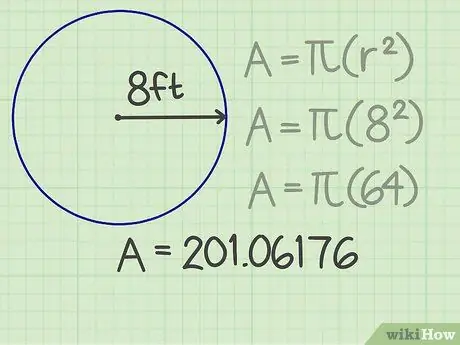
Krok 3. Výsledok vynásobte pí
Pi (π) je dôležité číslo používané v rôznych vzorcoch. Ak používate kalkulačku, stlačením klávesu pi získate skutočne presné výsledky. V opačnom prípade, aby boli vaše výpočty jednoduchšie, môžete za čiarkou zaokrúhliť pi na niekoľko číslic, napríklad 3, 14159. Keď toto číslo vynásobíte druhou mocninou polomeru, výsledkom je 201, 06176.
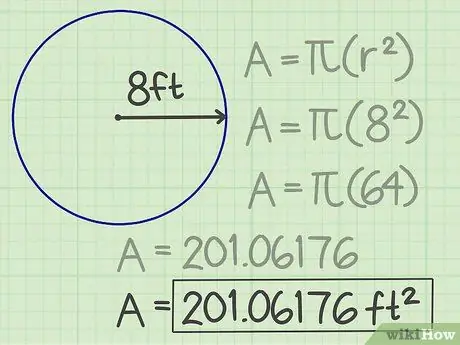
Krok 4. Zapíšte si výsledky
Získané číslo 201, 06176 je plocha kruhu. Jeho rozloha je teda 201 06176 stôp štvorcových.
Metóda 4 zo 7: Sektor (Juring)
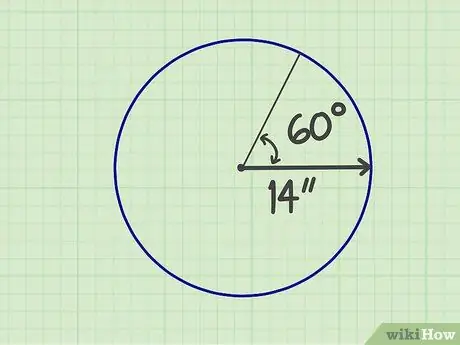
Krok 1. Zmerajte požadované čísla
Sektor je časť kruhu vytvoreného dvoma polomermi a hranou, takže tvar je ako vejár. Musíte poznať veľkosť polomeru a uhol, ktorý tvorí „ventilátor“. Predpokladajme napríklad, že sektor má polomer 14 palcov a uhol 60 stupňov.
V skutočnom svete to možno budete musieť zmerať sami, ale pokiaľ ide o domáce úlohy, učiteľ už zvyčajne zapísal čísla spolu s obrázkom tvaru
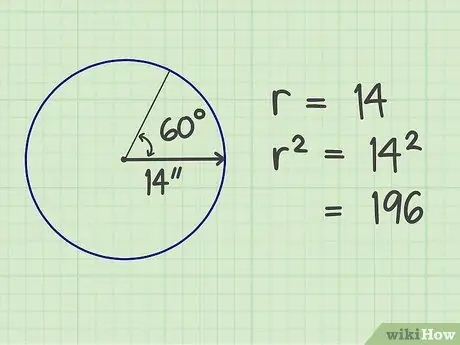
Krok 2. Štvorce prstov
Vynásobte počet polomerov sám. Výsledok je 196 (14x14).

Krok 3. Výsledok vynásobte pí
Pi (π) je dôležité číslo používané v rôznych vzorcoch. Ak používate kalkulačku, stlačením klávesu pi získate skutočne presné výsledky. V opačnom prípade, aby boli vaše výpočty jednoduchšie, môžete za čiarkou zaokrúhliť pi na niekoľko číslic, napríklad 3, 14159. Ak toto číslo vynásobíte druhou mocninou polomeru, výsledkom bude 615, 75164.

Krok 4. Rozdelte mieru uhla na 360
Rozdeľte uhol sektorového ventilátora o 360 (miera plného kruhového uhla). V prípade vyššie uvedeného príkladu je výsledok približne 0,166. Ak ho vypočítate pomocou kalkulačky, výsledok je v skutočnosti dlhší a iteračný, ale tu je zaokrúhlený, aby bol výpočet jednoduchší.

Krok 5. Vynásobte toto číslo predchádzajúcim číslom
Vynásobte číslo, ktoré získate po vydelení uhla 360, číslom, ktoré ste získali predtým po vynásobení pí štvorcom polomeru. pre vyššie uvedený príklad je výsledok 102, 214 (po zaokrúhlení).
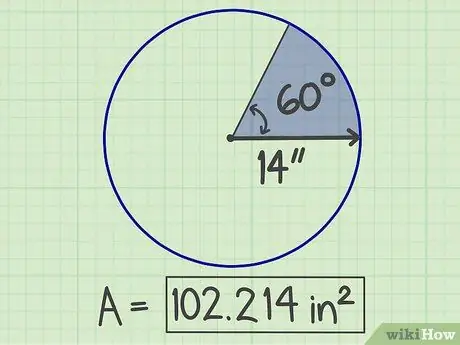
Krok 6. Zapíšte si výsledky
Získané číslo je plocha sektora, ktorá je 102 214 štvorcových palcov.
Metóda 5 zo 7: Elipsa
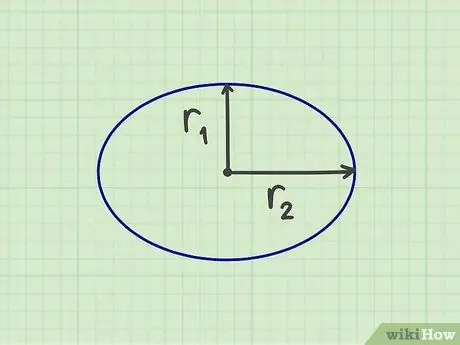
Krok 1. Zmerajte požadované číslo
Na výpočet plochy elipsy musíte zmerať dva „polomery“, a to krátky polomer a dlhý polomer, čo je polovica šírky a polovica výšky elipsy. Môžete tiež zmerať krátky polomer od stredu elipsy k najkratšej strane a dlhý polomer od stredu elipsy k najdlhšej strane. Krátky polomer by mal zvierať pravý uhol s dlhým polomerom.
V skutočnom svete to možno budete musieť zmerať sami, ale pokiaľ ide o domáce úlohy, učiteľ už zvyčajne zapísal čísla spolu s obrázkom tvaru
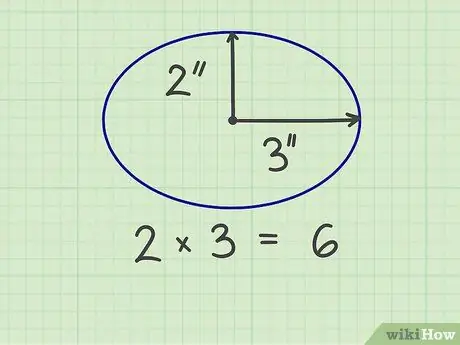
Krok 2. Vynásobte dva prsty
Elipsa je napríklad 6 palcov široká a 4 palce vysoká, takže polomery sú 3 palce a 2 palce. Keď sa tieto dve čísla vynásobia, výsledkom je 6 (3 x 2).

Krok 3. Výsledok vynásobte pí
Pi (π) je dôležité číslo používané v rôznych vzorcoch. Ak používate kalkulačku, stlačením klávesu pi získate skutočne presné výsledky. V opačnom prípade, aby boli vaše výpočty jednoduchšie, môžete za čiarkou zaokrúhliť pi na niekoľko číslic, napríklad 3, 14159. Keď toto číslo vynásobíte druhou mocninou polomeru, výsledok bude 18, 84954.
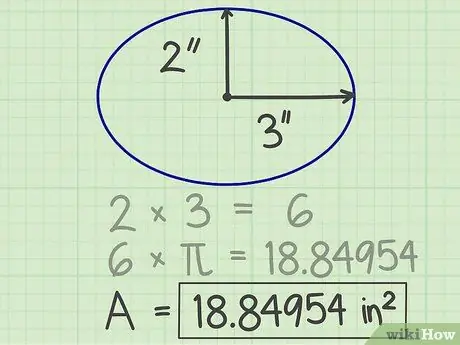
Krok 4. Zapíšte si výsledky
Číslo získané z vyššie uvedeného výpočtu je plocha elipsy. Vo vyššie uvedenom príklade je plocha elipsy 18,84954 štvorcových palcov.
Metóda 6 zo 7: Trojuholník
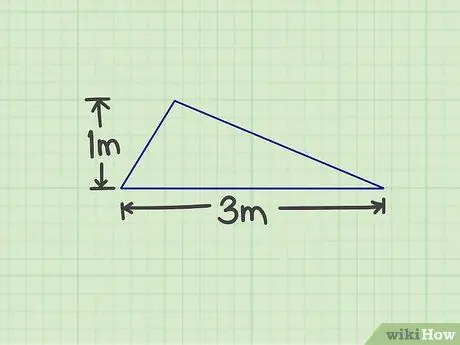
Krok 1. Zmerajte požadovaný počet
Musíte zmerať základňu a výšku trojuholníka. Základňou môže byť ktorákoľvek strana trojuholníka, pokiaľ však môžete merať výšku. Existuje napríklad trojuholník so základňou 3 m a výškou 1 m.
V skutočnom svete to možno budete musieť zmerať sami, ale pokiaľ ide o domáce úlohy, učiteľ už zvyčajne zapísal čísla spolu s obrázkom tvaru
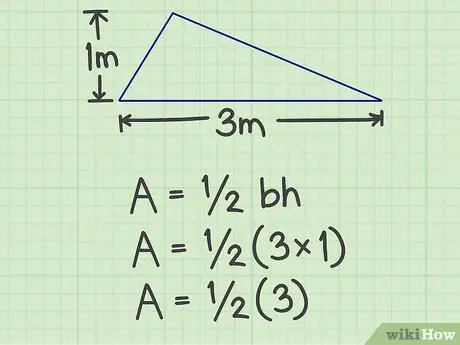
Krok 2. Vynásobte základňu výškou
V prípade vyššie uvedeného príkladu je výsledok 3 (3x1).
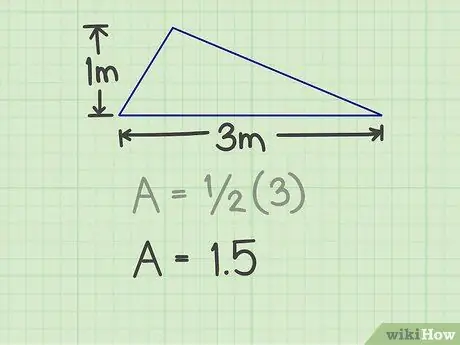
Krok 3. Výsledok vynásobte 1/2
Toto násobenie poskytne čísla 1, 5.
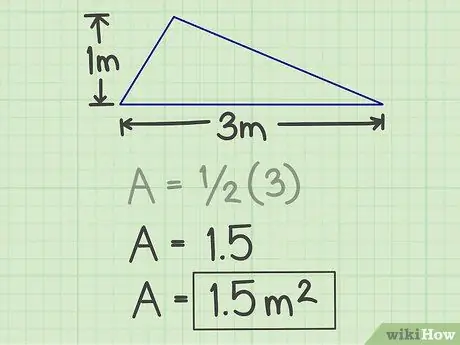
Krok 4. Zapíšte si výsledky
Číslo generované vyššie uvedeným výpočtom je plocha trojuholníka a v uvedenom príklade je jeho plocha 1,5 metra štvorcového.
Metóda 7 zo 7: Komplexná plochá stavba
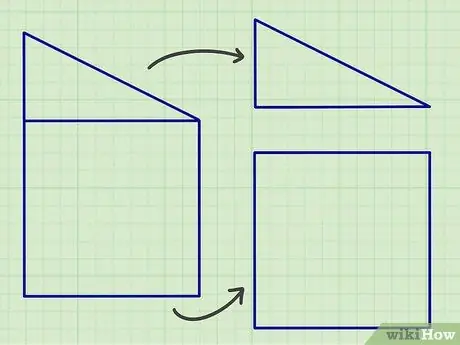
Krok 1. Komplexné rovinné tvary rozdeľte na časti pozostávajúce zo štandardných geometrických tvarov uvedených vyššie
Ak to, čo robíte, sú domáce úlohy, môže byť ľahké rozdeliť zložitý tvar na ploché tvary, o ktorých sme hovorili vyššie, ale v skutočnom svete možno budete musieť plochý tvar rozdeliť na veľa plochých tvarov, aby ste získali presný výsledok výpočtu..
Dobrým spôsobom, ako začať, je hľadať čiary, ktoré sú rovnobežné alebo zvierajú určitý uhol, pretože väčšina plochých tvarov je tvorená týmito tvarmi
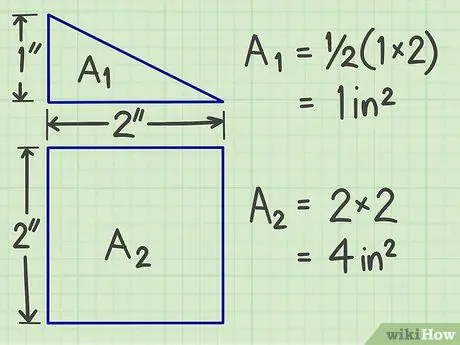
Krok 2. Vypočítajte plochu pre každú z rovinných figúr vyplývajúcich z oddelenia
Na získanie plochy každého plochého tvaru použite vyššie uvedené metódy.
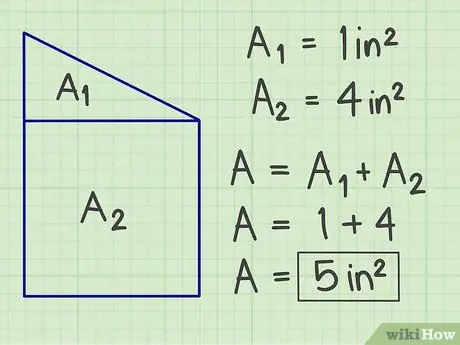
Krok 3. Sčítajte výsledky
Sčítajte všetky vypočítané oblasti a získajte celkovú plochu svojej zložitej rovinnej figúry.
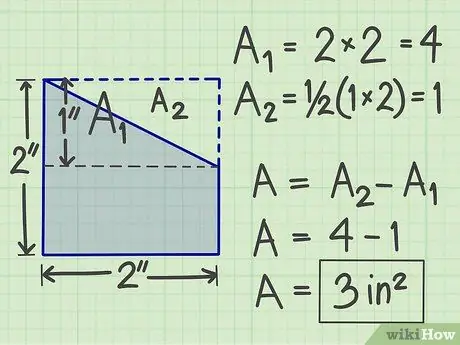
Krok 4. Použite inú metódu
Existuje mnoho ďalších spôsobov, ktoré môžete vyskúšať, v závislosti od tvaru zložitého plochého tvaru. Môžete k nemu napríklad napríklad pridať aj imaginárny rovinný tvar, aby sa stal štandardným geometrickým rovinným tvarom. Potom vypočítajte plochu a potom odčítajte plochu imaginárneho plochého tvaru, ktorý ste použili na pridanie.
Tipy
- Túto kalkulačku použite, ak potrebujete pomoc s riešením matematických výpočtov.
- Ak máte stále problémy, požiadajte o pomoc priateľa!
Pozor
- Vždy je lepšie dvakrát skontrolovať výsledky výpočtu a uistiť sa, že sú správne!
- Uistite sa, že jednotky, ktoré používate, sú pri výpočte rovnaké (cm, m, palce atď.), Aby ste sa kvôli zmiešaným jednotkám nepočítali nesprávne!






